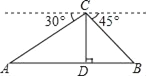
【题目】中央电视台体育频道用直升机航拍技术全程直播国际马拉松比赛.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为100米,点A、D、B在同一直线上,则A、B两点的距离是_____米.(保留根号)
参考答案:
【答案】100![]() +100
+100
【解析】分析:
由题意可知,在△ACD和△BCD中,∠CDA=∠CDB=90°,∠A=30°,∠B=45°,CD=100米,由此在△ACD和△BCD中分别求出AD和BD的长即可由AB=AD+BD求得A、B间的距离了.
详解:
由已知可得∠A=30°,∠B=45°,CD=100m,
∵CD⊥AB于点D.
∴在Rt△ACD中,∠CDA=90°,tanA=![]() ,
,
∴AD=![]() =
=![]() (m),
(m),
在Rt△BCD中,∠CDB=90°,∠B=45°
∴DB=CD=100m,
∴AB=AD+DB=100(![]() +1)m,
+1)m,
故答案为:(100![]() +100).
+100).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m.
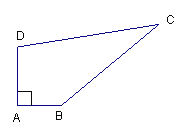
(1)求四边形ABCD的面积;
(2)学校计划在空地上种植草皮,若每平方米草皮需要200元,问学校需要投入多少资金买草皮
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD. -
科目: 来源: 题型:
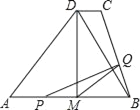
查看答案和解析>>【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)t(s)为何值时,点Q在BC上运动,t(s)为何值时,点Q在CD上运动;
(2)求S与t之间的函数关系式;
(3)当t为何值时,S有最大值,最大值是多少?
(4)当点Q在CD上运动时,直接写出t为何值时,△MPQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】早上,甲、乙、丙三人在同一条路上不同起点朝同方向以不同的速度匀速跑:
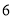 点
点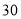 分时,乙在中间,丙在前,甲在后,且乙与甲、丙的距离相等:
分时,乙在中间,丙在前,甲在后,且乙与甲、丙的距离相等: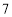 点时,甲追上乙;
点时,甲追上乙;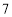 点
点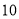 分时,甲追上丙;当乙追上丙时,若从
分时,甲追上丙;当乙追上丙时,若从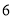 点
点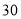 分起计时,丙跑的时间为___________分钟.
分起计时,丙跑的时间为___________分钟. -
科目: 来源: 题型:
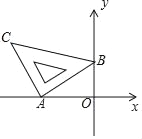
查看答案和解析>>【题目】如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(﹣2,0),B(0,1),则直线BC的函数表达式为_____.
相关试题

