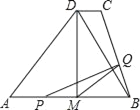
【题目】如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC﹣CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
(1)t(s)为何值时,点Q在BC上运动,t(s)为何值时,点Q在CD上运动;
(2)求S与t之间的函数关系式;
(3)当t为何值时,S有最大值,最大值是多少?
(4)当点Q在CD上运动时,直接写出t为何值时,△MPQ是等腰三角形.
参考答案:
【答案】(1)当0<t≤5且t≠4(s)时,点Q在BC上运动;当5≤t≤6(s)时,点Q在CD上运动;(2)当0<t<4时S=﹣![]() t2+
t2+![]() ;当4<t≤5时,S=
;当4<t≤5时,S=![]() t2﹣
t2﹣![]() ;当5<t≤6时,S=2t﹣8;(3)当t=6时,S取到最大值,最大值为4;(4)当t=
;当5<t≤6时,S=2t﹣8;(3)当t=6时,S取到最大值,最大值为4;(4)当t=![]() 秒时,△MPQ是等腰三角形.
秒时,△MPQ是等腰三角形.
【解析】试题分析:(1)过点C作CE⊥AB,垂足为E,可以证到四边形DCEM是矩形,从而可以求出![]() 的长,然后考虑不能构成
的长,然后考虑不能构成![]() 的情况,即可解决问题.
的情况,即可解决问题.
(2)由于点P在点M的两边时PM的表达式不同,点Q在线段BC和DC上时点Q到PM的距离的表达式不同,因此需分三种情况讨论,如图1、2、3所示,然后只需用t的代数式表示出PM及其边上的高,就可求出S与t之间的函数关系式.
(3)利用二次函数和一次函数的性质对(2)中的三种情况进行分析,即可解决问题.
(4)易证QM≠MP,QP≠MP.若![]() 是等腰三角形,只能是
是等腰三角形,只能是![]() 由
由![]() 可得:
可得: ![]() 再由
再由![]() 可得到关于t的方程,解这个方程即可解决问题.
可得到关于t的方程,解这个方程即可解决问题.
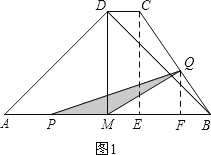
试题解析:(1)过点C作CE⊥AB,垂足为E,如图1,
∵DA=DB,AM=BM,
∴DM⊥AB.
∵CE⊥AB,
∴![]()
∴CE∥DM.
∵DC∥ME,CE∥DM, ![]()
∴四边形DCEM是矩形,
∴CE=DM=4,ME=DC=1.
∵AM=BM,AB=8,
∴AM=BM=4.
∴BE=BMME=3.
∵![]()
∴CB=5.
∵当t=4时,点P与点M重合,不能构成△MPQ,
∴t≠4.
∴当![]() 且t≠4(s)时,点Q在BC上运动;当
且t≠4(s)时,点Q在BC上运动;当![]() (s)时,点Q在CD上运动.
(s)时,点Q在CD上运动.
(2)①当0<t<4时,点P在线段AM上,点Q在线段BC上,
过点Q作QF⊥AB,垂足为F,如图1,
∵QF⊥AB,CE⊥AB,
∴![]()
∴QF∥CE.
∴△QFB∽△CEB.
∴![]()
∵CE=4,BC=5,BQ=t,
∴![]()
∴![]()
∵PM=AMAP=4t,
∴![]()
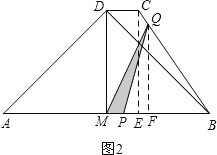
②当![]() 时,点P在线段BM上,点Q在线段BC上,
时,点P在线段BM上,点Q在线段BC上,
过点Q作QF⊥AB,垂足为F,如图2,
∵QF⊥AB,CE⊥AB,
∴![]()
∴QF∥CE.
∴△QFB∽△CEB.
∴![]()
∵CE=4,BC=5,BQ=t,
∴![]()
∴![]()
∵PM=APAM=t4,
∴![]()
③当![]() 时,点P在线段BM上,点Q在线段DC上,
时,点P在线段BM上,点Q在线段DC上,
过点Q作QF⊥AB,垂足为F,如图3,
此时QF=DM=4.
∵PM=APAM=t4,
∴![]()
综上所述:当![]() 当
当![]() 时,
时, ![]() 当
当![]() 时,S=2t8.
时,S=2t8.
(3)①当0<t<4时, ![]()
∵![]() 0<2<4,
0<2<4,
∴当t=2时,S取到最大值,最大值为![]()
②当![]() 时,
时, ![]() 对称轴为x=2.
对称轴为x=2.
∵![]()
∴当x>2时,S随着t的增大而增大,
∴当t=5时,S取到最大值,最大值为![]()
③当![]() 时,S=2t8.
时,S=2t8.
∵2>0,
∴S随着t的增大而增大,
∴当t=6时,S取到最大值,最大值为2×68=4.
综上所述:当t=6时,S取到最大值,最大值为4.
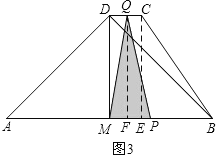
(4)当点Q在CD上运动即![]() 时,如图3,
时,如图3,
则有![]()
![]() ,即
,即![]()
∵MP=t4<64,即MP<2,
∴QM≠MP,QP≠MP.
若△MPQ是等腰三角形,则QM=QP.
∵QM=QP,QF⊥MP,
∴MF=PF=12MP.
∵MF=DQ=5+1t=6t,MP=t4,
∴![]()
解得: ![]()
∴当t=![]() 秒时,△MPQ是等腰三角形.
秒时,△MPQ是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数轴,根据数形结合思想,回答下列问题:

(1)已知|x|=3,则x的值是 .
(2)数轴上表示2和6两点之间的距离是 ,数轴上表示1和﹣2的两点之间的距离为 ;
(3)数轴上表示x和1两点之间的距离为 ,数轴上表示x和﹣3两点之间的距离为
(4)若x表示一个实数,且﹣5<x<3,化简|x﹣3|+|x+5|= ;
(5)|x+3|+|x﹣4|的最小值为 ,|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|+|x﹣5|的最小值为 .
(6)|x+1|﹣|x﹣3|的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学有一块四边形的空地ABCD,如图所示,经测量∠A=90°,AB=6m,BC=24m,CD=26m,DA=8m.
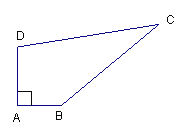
(1)求四边形ABCD的面积;
(2)学校计划在空地上种植草皮,若每平方米草皮需要200元,问学校需要投入多少资金买草皮
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,过点O作两条射线OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度数.
(2)若∠1=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD. -
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台体育频道用直升机航拍技术全程直播国际马拉松比赛.如图,在直升机的镜头下,观测马拉松景观大道A处的俯角为30°,B处的俯角为45°.如果此时直升机镜头C处的高度CD为100米,点A、D、B在同一直线上,则A、B两点的距离是_____米.(保留根号)
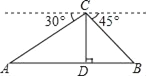
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果A、B、C三点在同一直线上,且线段AB=6 cm,BC=4 cm,若M,N分别为AB,BC的中点,那么M,N两点之间的距离为( )
A. 5 cm B. 1 cm C. 5或1 cm D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】早上,甲、乙、丙三人在同一条路上不同起点朝同方向以不同的速度匀速跑:
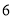 点
点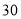 分时,乙在中间,丙在前,甲在后,且乙与甲、丙的距离相等:
分时,乙在中间,丙在前,甲在后,且乙与甲、丙的距离相等: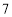 点时,甲追上乙;
点时,甲追上乙;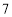 点
点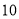 分时,甲追上丙;当乙追上丙时,若从
分时,甲追上丙;当乙追上丙时,若从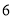 点
点 分起计时,丙跑的时间为___________分钟.
分起计时,丙跑的时间为___________分钟.
相关试题

