【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y= ![]() 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 
参考答案:
【答案】12
【解析】解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H,

∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=2,设C(m+1,n),D(m,n+2),
则(m+1)n=m(n+2)=k,
解得n=2m,则D的坐标是(m,2m+2),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得
![]() ,
,
由①得:a=b,代入②得:mb+b=2m+2,
即b(m+1)=2(m+1),解得b=2,
则 ![]() ,
,
∴y=2x+2,E(0,2),BE=4,
∴S△ABE= ![]() ×BE×AO=2,
×BE×AO=2,
∵S四边形BCDE=5S△ABE=5× ![]() ×4×1=10,
×4×1=10,
∵S四边形BCDE=S△ABE+S四边形BEDM=10,
即2+4×m=10,
解得m=2,
∴n=2m=4,
∴k=(m+1)n=3×4=12.
所以答案是:12.
【考点精析】掌握确定一次函数的表达式和比例系数k的几何意义是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,b)在双曲线y=
 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .
上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组
视力
人数
A
3.95≤x≤4.25
3
B
4.25<x≤4.55
C
4.55<x≤4.85
18
D
4.85<x≤5.15
8
E
5.15<x≤5.45
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
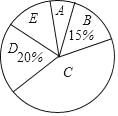
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:
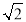 的有理化因式是
的有理化因式是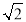 ;
;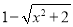 的有理化因式是
的有理化因式是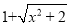 .
.(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:
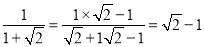 ,
,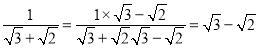
问题解决:
(1)填空:
 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)(2)直接写出下列各式分母有理化的结果:
①
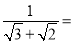 _____;②
_____;②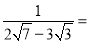 ______.
______.(3)计算:
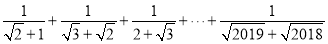 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=
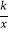 (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=  ,则BN的长为 .
,则BN的长为 . 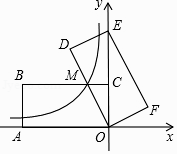
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
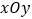 中,已知直线
中,已知直线 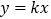 (
(  )分别交反比例函数
)分别交反比例函数 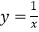 和
和 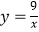 在第一象限的图象于点
在第一象限的图象于点 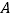 ,
, 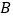 ,过点
,过点 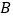 作
作  轴于点
轴于点 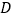 ,交
,交 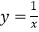 的图象于点
的图象于点 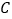 ,连结
,连结 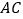 .若
.若 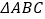 是等腰三角形,则
是等腰三角形,则  的值是 .
的值是 . 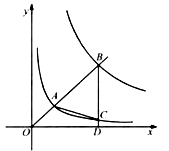
-
科目: 来源: 题型:
查看答案和解析>>【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题:
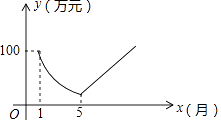
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
相关试题

