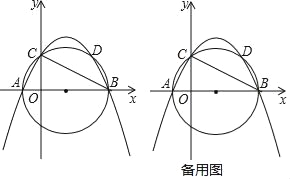
【题目】如图,已知二次函数y=ax2+bx+c(a<0,c>0)与x轴交于点A、B,与y轴交于点C,且以AB为直径的圆经过点C.
(1)若点A(﹣2,0),点B(8,0),求ac的值;
(2)若点A(x1,0),B(x2,0),试探索ac是否为定值?若是,求出这个定值;若不是,请说明理由.
(3)若点D是圆与抛物线的交点(D与 A、B、C 不重合),在(1)的条件下,坐标轴上是否存在一点P,使得以P、B、C为顶点的三角形与△CBD相似?若存在,请直接写出点P坐标;若不存在,请说明理由.
参考答案:
【答案】(1)ac=﹣1;(2)ac的值是定值,为﹣1;(3)P的坐标为(2,0)或(﹣![]() ,0)或(0,
,0)或(0, ![]() )或(0,16).
)或(0,16).
【解析】试题分析:(1)设圆心点为M,利用A、B的坐标求出圆的半径,然后根据勾股定理求出OC的长,求得C点,然后利用x轴的交点式y=a(x+2)(x﹣8)代入C点的坐标得到函数的解析式即可求解;
(2)根据坐标系中交点的坐标,利用三角形相似的判定得到△OAC∽△OCB,再根据相似三角形的性质,结合一元二次方程根与系数的关系求出ac=-1是一个定值;
(3)根据题意,分为点P在x轴上或点P在y轴上两种情况,结合相似三角形的判定与性质可求P点的坐标.
试题解析:(1)设圆心为点M,
∵A(﹣2,0),B(8,0),
∴M(3,0),⊙M的半径为5,
∴OC=![]() =4,
=4,
∴C(0,4),
设抛物线解析式为y=a(x+2)(x﹣8),
∵点C在抛物线上,
∴a×2×(﹣8)=4,
∴a=﹣![]() ,
,
∴y=﹣![]() (x+2)(x﹣8)=﹣
(x+2)(x﹣8)=﹣![]() x2+
x2+![]() x+4,
x+4,
∴a=﹣![]() ,b=4,
,b=4,
∴ac=﹣1;
(2)ac的值是定值,为﹣1,
理由:∵点A(x1,0),B(x2,0),
∴OA=x1,OB=x2,OC=c,
∵∠OAC+∠OCA=90°,∠OCB+∠OCA=90°,
∴∠OAC=∠OCB,
∵∠AOC=∠BOC=90°,
∴△OAC∽△OCB,
∴![]() ,
,
∴OC2=OAOB,
∴c2=﹣x1x2,
令y=0时,0=ax2+bx+c,
∴x1x2=![]() ,
,
∴c2=﹣![]() ,
,
∴ac=﹣1;
(3)∵点D是圆与抛物线的交点(D与 A、B、C 不重合),C(0,4),
∴D(6,4),即:CD∥AB,
当点P在x轴上时,如图1,设点P的坐标为(m,0),
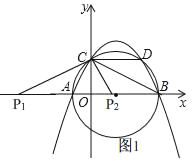
∵C(0,4),D(6,4),B(8,0),
∴BC=4![]() ,CD=6,BP=8﹣m,
,CD=6,BP=8﹣m,
∵CD∥AB,
∴∠BCD=∠ABC,
∵以P、B、C为顶点的三角形与△CBD相似,
∴①![]() ,
,
∴![]() ,
,
∴m=2,
∴P2(2,0),
或②![]() ,
,
∴![]() ,
,
∴m=﹣![]() ,
,
∴P1(﹣![]() ,0),
,0),
当点P在y轴上时,如图2,
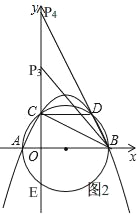
∵CD∥AB,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴∠ABD=∠BCO,
∵CD∥AB,
∴∠BDC+∠ABC=180°,
∵∠BCO+∠BCy=180°,
∴∠BDC=∠BCy,
设P(0,n),
∵C(0,4),D(6,4),B(8,0),
∴BC=4![]() ,CD=6,BD=2
,CD=6,BD=2![]() ,CP=n﹣4,
,CP=n﹣4,
∵以P、B、C为顶点的三角形与△CBD相似,
∴①![]() ,
,
∴![]() ,
,
∴n=![]() ,
,
∴P3(0,![]() )
)
或②![]() ,
,
∴![]() ,
,
∴n=16,
∴P4(0,16),
即:满足条件的点P的坐标为(2,0)或(﹣![]() ,0)或(0,
,0)或(0,![]() )或(0,16).
)或(0,16).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,且DG⊥CE,垂足为点G.
(1)求证:DC=BE;
(2)若∠AEC=54°,求∠BCE的度数.

-
科目: 来源: 题型:
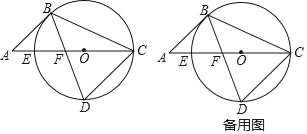
查看答案和解析>>【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=
 ∠EFD=34°( )
∠EFD=34°( )又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】作出函数y=﹣x+3的图象,并利用图象回答问题:
(1)当y<0时,x的取值范围为_____;
(2)当﹣2<x<2时,y的取值范围为_____;
(3)图象与直线y=x﹣1的交点坐标为______;这两条直线与y轴围成的三角形面积为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE平分∠CAD,AE∥BC,O为△ABC内一点,∠OBC=∠OCB.求证:∠ABO=∠ACO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角形的直角顶点0按图1方式叠放在一起(其中∠C=30°,∠CDO=60°;∠OAB=∠OBA=45°).△COD绕着点O顺时针旋转一周,旋转的速度为每秒10°,若旋转时间为t秒,请回答下列问题:(请直接写出答案)
(1)当0<t<9时(如图2),∠BOC与∠AOD有何数量关系
(2)当t为何值时,边OA∥CD?

相关试题

