【题目】如图,AE平分∠CAD,AE∥BC,O为△ABC内一点,∠OBC=∠OCB.求证:∠ABO=∠ACO.

参考答案:
【答案】见解析
【解析】
根据平行线的性质,可得到:∠CAE=∠ACB,∠DAE=∠ABC,因为AE平分∠CAD,所以有:∠CAE=∠DAE,从而得到:∠ACB=∠ABC,又因为∠OBC=∠OCB,∠ABC=∠ABO+∠OBC,∠ACB=∠ACO+∠OCB,从而可得证,由此来解答本题即可.
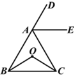
解:∵AE∥BC,
∴∠CAE=∠ACB,∠DAE=∠ABC,
∵AE平分∠CAD,
∴∠CAE=∠DAE,
∴∠ACB=∠ABC,
∵∠OBC=∠OCB,∠ABC=∠ABO+∠OBC,∠ACB=∠ACO+∠OCB,
∴∠ABO=∠ACO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角形的直角顶点0按图1方式叠放在一起(其中∠C=30°,∠CDO=60°;∠OAB=∠OBA=45°).△COD绕着点O顺时针旋转一周,旋转的速度为每秒10°,若旋转时间为t秒,请回答下列问题:(请直接写出答案)
(1)当0<t<9时(如图2),∠BOC与∠AOD有何数量关系
(2)当t为何值时,边OA∥CD?

-
科目: 来源: 题型:
查看答案和解析>>【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ②
②  ③
③ 
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:
,请结合(1)中选取的函数关系式继续解决下列问题:
①市交通运行监控平台显示,当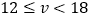 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
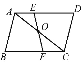
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
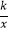 在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
(1)求E点的坐标及k的值;
(2)求△OCD的面积.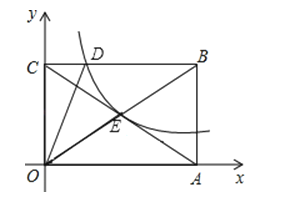
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.

解:∵AB∥CD(已知)
∴∠EFD=∠AEF( )
∵∠AEF=68°(已知)
∴∠EFD=∠AEF=68°( )
∵FG平分∠EFD(已知)
所以∠EFG=∠GFD=
 ∠EFD=34°( )
∠EFD=34°( )又因为KF⊥FG( )
所以∠KFG=90°( )
所以∠KFC=180°-∠GFD-∠KFG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用完全平方公式进行因式分解,解答下列问题:
 因式分解:
因式分解: .
. 填空: ①当
填空: ①当 时,代数式
时,代数式 _ .
_ .②当
 _ 时,代数式
_ 时,代数式 .
.③代数式
 的最小值是_ .
的最小值是_ . 拓展与应用:求代数式
拓展与应用:求代数式 的最小值.
的最小值.
相关试题

