【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
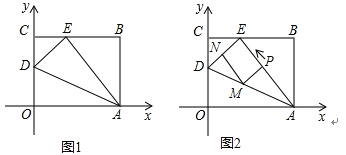
(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
参考答案:
【答案】(1)(0,![]() );(2,4).(2) S矩形PMNE=-
);(2,4).(2) S矩形PMNE=-![]() (t-
(t-![]() )2+
)2+![]() ,当t=
,当t=![]() 时,S矩形PMNE有最大值
时,S矩形PMNE有最大值![]() .(3)当t=
.(3)当t=![]() 时,DP平分∠EDA.(4)当t=
时,DP平分∠EDA.(4)当t=![]() 或t=2
或t=2![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(![]() ,
,![]() )或(5-2
)或(5-2![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据折叠的性质可知:AE=OA,OD=DE,那么可在直角三角形ABE中,用勾股定理求出BE的长,进而可求出CE的长,也就得出了E点的坐标.在直角三角形CDE中,CE长已经求出,CD=OC-OD=4-OD,DE=OD,用勾股定理即可求出OD的长,也就求出了D点的坐标;
(2)很显然四边形PMNE是个矩形,可用时间t表示出AP,PE的长,然后根据相似三角形APM和AED求出PM的长,进而可根据矩形的面积公式得出S,t的函数关系式,根据函数的性质即可得出S的最大值及对应的t的值;
(3)由DP是∠EDA的角平分线可知:PE=PM,然后结合相似三角形的性质列出关于t的方程,最后再求解即可;
(4)本题要分三种情况进行讨论:(Ⅰ)ME=MA时,此时MP为三角形ADE的中位线,那么AP=![]() ,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.(Ⅱ)当MA=AE时,先在直角三角形OAD中求出斜边AD的长,然后根据相似三角形AMP和ADE来求出AP,MP的长,也就能求出t的值.根据折叠的性质,此时AF=AP,MF=MP,也就求出了M的坐标;(Ⅲ)EM=EA的情况不成立.
,据此可求出t的值,过M作MF⊥OA于F,那么MF也是三角形AOD的中位线,M点的横坐标为A点横坐标的一半,纵坐标为D点纵坐标的一半.由此可求出M的坐标.(Ⅱ)当MA=AE时,先在直角三角形OAD中求出斜边AD的长,然后根据相似三角形AMP和ADE来求出AP,MP的长,也就能求出t的值.根据折叠的性质,此时AF=AP,MF=MP,也就求出了M的坐标;(Ⅲ)EM=EA的情况不成立.
试题解析:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∵在Rt△ABE中,AE=AO=5,AB=4,BE=![]() =3.
=3.
∴CE=2.
∴E点坐标为(2,4).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD.
∴(4-OD)2+22=OD2.
解得:OD=![]() .
.
∴D点坐标为(0,![]() ).
).
(2)∵PM∥ED,
∴△APM∽△AED.
∴![]() ,
,
∴PM=![]() .
.
又∵AP=t,ED=![]() ,AE=5,
,AE=5,
∴PM=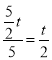 .
.
∵PM∥DE,MN∥EP,
∴四边形NMPE为平行四边形.
又∵∠DEA=90°,
∴四边形PMNE为矩形.
∴S矩形PMNE=PMPE=![]() ×(5-t)=-
×(5-t)=-![]() t2+
t2+![]() t.
t.
∴S矩形PMNE=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
又∵0<![]() <5.
<5.
∴当t=![]() 时,S矩形PMNE有最大值
时,S矩形PMNE有最大值![]() .
.
(3)∵四边形NMPE是矩形,
∴PM⊥AD,PE⊥DE.
又∵DP平分∠EDA,
∴PE=PM.
由(2)可知:PM=![]() ,PE=5-t.
,PE=5-t.
∴![]() =5-t.
=5-t.
解得:t=![]() .
.
∴当t=![]() 时,DP平分∠EDA.
时,DP平分∠EDA.
(4)(Ⅰ)若以AE为等腰三角形的底,则ME=MA(如图①)
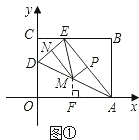
在Rt△AED中,ME=MA,
∵PM⊥AE,
∴P为AE的中点,
∴t=AP=![]() AE=
AE=![]() .
.
又∵PM∥ED,
∴M为AD的中点.
过点M作MF⊥OA,垂足为F,则MF是△OAD的中位线,
∴MF=![]() OD=
OD=![]() ,OF=
,OF=![]() OA=
OA=![]() ,
,
∴当t=![]() 时,(0<
时,(0<![]() <5),△AME为等腰三角形.
<5),△AME为等腰三角形.
此时M点坐标为(![]() ,
,![]() ).
).
(Ⅱ)若以AE为等腰三角形的腰,则AM=AE=5(如图②)
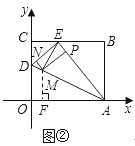
在Rt△AOD中,AD=![]() =
=![]() .
.
过点M作MF⊥OA,垂足为F.
∵PM∥ED,
∴△APM∽△AED.
∴![]() .
.
∴t=AP=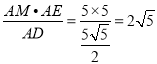 .
.
∴PM=![]() t=
t=![]() .
.
∴MF=MP=![]() ,OF=OA-AF=OA-AP=5-2
,OF=OA-AF=OA-AP=5-2![]() ,
,
∴当t=2![]() 时,(0<2
时,(0<2![]() <5),此时M点坐标为(5-2
<5),此时M点坐标为(5-2![]() ,
,![]() ).
).
(Ⅲ)根据图形可知EM=EA的情况不成立.
综合综上所述,当t=![]() 或t=2
或t=2![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(![]() ,
,![]() )或(5-2
)或(5-2![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:

例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该户居民5、6两个月共交水费多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一次函数y=kx+b的图象.
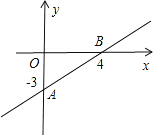
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图)。由于三月份展开促销活动,男女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装的销售总收入为20万元。

(1)二月份销售收入为_______万元。三月份销售收入为______万元。
(2)二月份男女服装的销售收入分别是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
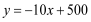 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润为2000元,那么小明每月的成本需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】
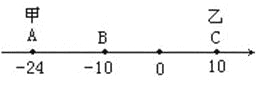
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是____________.
相关试题

