【题目】
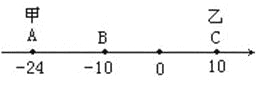
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是____________.
参考答案:
【答案】(1)3.4秒 (2)2或者5秒(3)-44
【解析】试题分析:(1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解;
(3)分①原点O是甲蚂蚁P与乙蚂蚁Q两点的中点;②乙蚂蚁Q是甲蚂蚁P与原点O两点的中点;③甲蚂蚁P是乙蚂蚁Q与原点O两点的中点,三种情况讨论即可求解.
试题解析:(1)设x秒后甲与乙相遇,则
4x+6x=34,
解得x=3.4,
甲乙在3.4秒后相遇.
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
(3)①甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:-24+4×2-4y;乙表示的数为:10-6×2-6y,
依据题意得:-24+4×2-4y=10-6×2-6y,
解得:y=7,
相遇点表示的数为:-24+4×2-4y=-44(或:10-6×2-6y=-44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:-24+4×5-4y;乙表示的数为:10-6×5-6y,
依据题意得:-24+4×5-4y=10-6×5-6y,
解得:y=-8(不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.
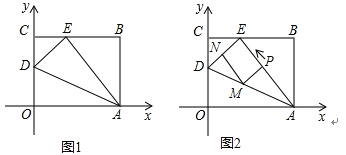
(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图)。由于三月份展开促销活动,男女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装的销售总收入为20万元。

(1)二月份销售收入为_______万元。三月份销售收入为______万元。
(2)二月份男女服装的销售收入分别是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:
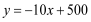 ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的80%.(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润为2000元,那么小明每月的成本需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市市政府出台了《深化出租汽车行业改革的指导意见》,指导意见中有一条特别引人瞩目:萧山区、余杭区、富阳区等地的出租车价格将与杭州主城区一致.未来,萧山出租车起步价上调已成定局.下表是目前及未来调价后萧山区的出租车收费标准:
目前萧山区出租车收费标准
起步价(2公里及以内)
(元)
2公里外至6公里
(元/公里)
6公里外
(元/公里)
6
2.4
3.6
未来调价后萧山出租车收费标准
起步价(3公里及以内)
(元)
3公里外至10公里
(元/公里)
10公里外
(元/公里)
11
2.4
3.75
(1)小慧家到学校有4公里,小慧坐出租车从家到学校,按目前收费标准小慧应付车费 元,按未来调价后的收费标准应付车费 元.
(2)设坐出租车x(x>6)公里.
①按目前收费标准应付车费多少元;(用x的代数式表示,并化简)
②若按未来调价后的收费标准,当6<x≤10时,应付车费多少元?当x>10时,又应付车费多少元?(分别用x的代数式表示,并化简)
(3)求坐出租车多少公里时,目前收费标准与未来调价后的收费相同?若出租车收费时,出租车路程不足1公里按1公里计(例如4.1公里按5公里收费),请直接写出坐多少公里出租车时,费用还是未来调价后的收费更合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
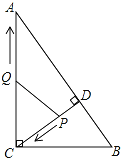
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价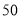 元售出,那么每天可售出50个.根据销售经验,售价每提高
元售出,那么每天可售出50个.根据销售经验,售价每提高 元.销售量相应减少1个。
元.销售量相应减少1个。(1)假设销售单价提高
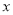 元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。
元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。(2)假设每天销售这种篮球所得利润为y ,请用含
 的代数式表示y。
的代数式表示y。(3)假如你是商场老板,为了在出售这种篮球时获得最大利润,你该提高多少元?最大利润是多少?请说明理由。
相关试题

