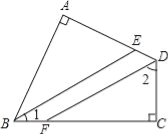
【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的性质得出∠1=∠ABE,∠2=∠ADF。根据四边形内角和定理可得∠ABC+∠ADC=180°,即2(∠1+∠2)=180°,从而得出答案;(2)、根据三角形内角和定理可得∠DFC+∠2=90°,结合第一题的结论得出∠1=∠DFC,从而得出答案.
试题解析:(1)、∵BE,DF分别是∠ABC,∠ADC的平分线, ∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°, ∴∠ABC+∠ADC=180°, ∴2(∠1+∠2)=180°, ∴∠1+∠2=90°;
(2)、在△FCD中,∵∠C=90°, ∴∠DFC+∠2=90°, ∵∠1+∠2=90°,
∴∠1=∠DFC, ∴BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm
B.等于12cm
C.小于6cm
D.大于12cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中
 ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。

-
科目: 来源: 题型:
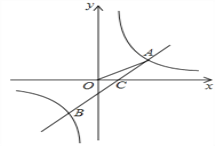
查看答案和解析>>【题目】如图,反比例函数y=
 与反比例函数y=k2
与反比例函数y=k2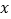 +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与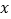 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=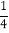 。
。(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A.某人在岸边的B处测得A在B的北偏东60°的方向上.然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:
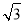 ≈1.732)
≈1.732)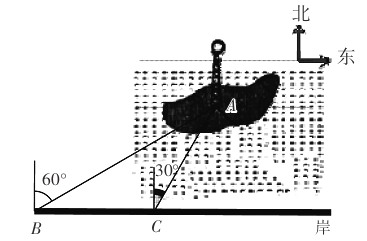
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面给出四边形ABCD中的∠A、∠B、∠C、∠D的度数之比,能判定四边形ABCD是平行四边形的是( ).
A. 3:4:4:3B. 4:3:4:3C. 4:3:2:1D. 2:2:3:3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.在这次活动中.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他类共四类),并将调查结果绘制成如下两幅不完整的统计图.请你结合图中的信息解答下列问题:

(1)求被调查的学生人数;
(2)请补全条形统计图;
(3)若该校有1200名学生,试估计全校最喜爱文学类图书的学生人数.
相关试题

