【题目】在△ABC中![]() ,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
,AO=BO,直线MN经过点O, 且AC⊥MN于C,BD⊥MN于D
(1) 当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
(2) 当直线MN绕点O旋转到图②的位置时,求证:CD=AC-BD;
(3) 当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明。

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)CD=BD-AC,证明见解析.
【解析】试题分析:(1)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC+BD;
(2)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC-BD;
(3)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=BD-AC.
试题解析:(1)如图1,
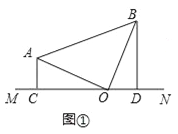
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
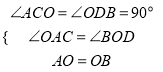
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=AC+BD;
(2)如图2,
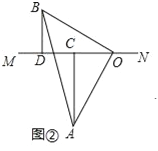
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
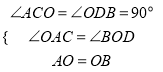 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OD﹣OC=AC﹣BD,即CD=AC﹣BD.
(3)如图3,

∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
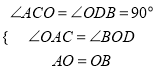 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OC﹣OD=BD﹣AC,
即CD=BD﹣AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】既是中心对称图形,又是轴对称图形的是( )
A.平行四边形
B.正五边形
C.菱形
D.等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在市委宣传部举办的以“弘扬社会主义核心价值观”为主题的演讲比赛中,其中10位参赛选手的成绩如下:9.3;9.5;8.9;9.3;9.5;9.5;9.7;9.4;9.5,这组数据的众数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm
B.等于12cm
C.小于6cm
D.大于12cm -
科目: 来源: 题型:
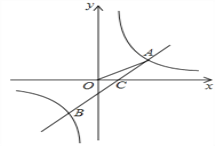
查看答案和解析>>【题目】如图,反比例函数y=
 与反比例函数y=k2
与反比例函数y=k2 +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=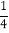 。
。(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
-
科目: 来源: 题型:
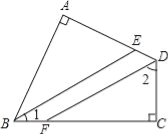
查看答案和解析>>【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,郴州北湖公园的小岛上有为了纪念唐代著名诗人韩愈而建的韩愈铜像,其底部为A.某人在岸边的B处测得A在B的北偏东60°的方向上.然后沿岸边直行200米到达C处,再次测得A在C的北偏东30°的方向上(其中A,B,C在同一平面上).求这个铜像底部A到岸边BC的距离(结果精确到0.1米,参考数据:
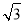 ≈1.732)
≈1.732)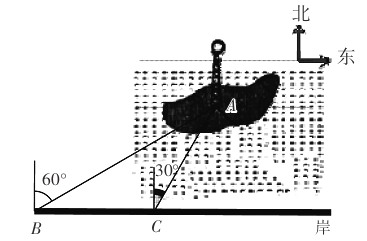
相关试题

