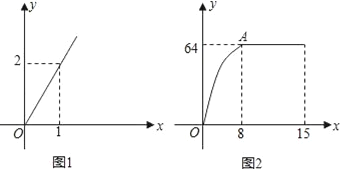
【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
参考答案:
【答案】(1)老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式为y=2x;
(2)学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式为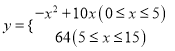 ;
;
(3)老师在课堂用于精讲的时间为33分钟,学生当堂检测的时间为7分钟时,学习收益总量最大.
【解析】(1)由图设该函数解析式为y=kx,即可依题意求出y与x 的函数关系式.
(2)本题涉及分段函数的知识,需要注意的是x的取值范围依照分段函数的解法解出即可.
(3)设学生当堂检测的时间为x分钟(0≤≤15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟,用配方法的知识解答该题即可.
解:(1)设y=kx,把(1,2)代入,得k=2.∴y=2x.
自变量x的取值范围是:0≤x≤40.
(2)当0≤x≤8时,设y=a(x-8)2+64,
y=
把(0,0)代入,得64a+64=0,a=-1.
∴y=-(x-8)2+64=-x2+16x.
当8=x=15时,y=64
(3)设学生当堂检测的时间为x分钟(0=x=15),学生的学习收益总量为W,则老师在课堂用于精讲的时间为(40-x)分钟.
当0=x=8时,w=-x2+16x+2(40-x)=-x2+14x+80=-(x-7)2+129.
∴当x=7时,W 最大=129.
当8=x=15时,W=64+2(40-x)=-2x+144.
∵W随x的增大而减小, ∴当x=8时,W最大=128
综合所述,当x=7时,W最大=129,此时40-x=33.
即老师在课堂用于精讲的时间为33分钟,学生当堂检测的时间为7分钟时,学习收益总量最大.

“点睛”本题考查了待定系数法求一次函数的解析式的运用,二次函数的运用,顶点式求二次函数的最大值的运用,解答时求出二次函数的解析式是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.
(1)如图(1),连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
A.20°
B.30°
C.70°
D.110° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边长分别为3、5,且周长为整数,则这样的三角形共有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据天气预报2018年4月12日大田县的最高气温是32℃,最低气温是21℃,则当天大田县气温t(℃)的变化范围是( )
A. t>21 B. t<32 C. 21<t<32 D. 21≤t≤32
-
科目: 来源: 题型:
查看答案和解析>>【题目】若干个苹果分给x个小孩,如果每人分3个,那么余7个;如果每人分5个,那么最后一人分到的苹果不足5个,则x满足的不等式组为( )
A. 0<(3x+7)﹣5(x﹣1)≤5 B. 0<(3x+7)﹣5(x﹣1)<5
C. 0≤(3x+7)﹣5(x﹣1)<5 D. 0≤(3x+7)﹣5(x﹣1)≤5
相关试题

