【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.
(1)如图(1),连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图(2),动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
参考答案:
【答案】
(1)证明:证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵AC的垂直平分线EF,
∴OA=OC,
在△AOE和△COF中,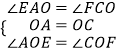 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
∴AF=FC,
设AF=xcm,
则CF=xcm,BF=(8﹣x)cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴在Rt△ABF中,
由勾股定理得:42+(8﹣x)2=x2 ,
解得x=5,即AF=5cm
(2)解:显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
如图所示: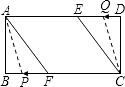
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得t= ![]() .
.
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t= ![]() 秒.
秒.
【解析】(1)根据矩形的性质及垂直平分线的性质得出∠EAO=∠FCO,OA=OC,再证明△AOE≌△COF,得出OE=OF,再根据EF⊥AC,可证得四边形AFCE是菱形.由菱形的性质得出AF=CF,然后在Rt△ABF中,设未知数,根据勾股定理建立方程求解即可得出AF的长。
(2)根据已知结合图形,分情况讨论:可知当P点在AF上时,Q点在CD上或P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时,以A、C、P、Q四点为顶点不能构造平行四边形;只有当P点在BF上、Q点在ED上时,才能构成平行四边形,得出PC=QA,建立关于t的方程求解即可。
【考点精析】关于本题考查的勾股定理的概念和平行四边形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数
 的图象和矩形ABCD在第一象限,AD平行于
的图象和矩形ABCD在第一象限,AD平行于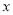 轴,且AB=2,AD=4,点A的坐标为(2,6).
轴,且AB=2,AD=4,点A的坐标为(2,6).
(1)直接写出B、C、D三点的坐标.
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点M(a-3,a+4),点N(5,9),若MN∥y轴,则a=____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果(x+1)(x+m)的乘积中不含x的一次项,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆内接四边形ABCD中,已知∠A=70°,则∠C=( )
A.20°
B.30°
C.70°
D.110° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

-
科目: 来源: 题型:
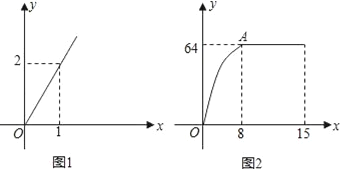
查看答案和解析>>【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
相关试题

