【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

参考答案:
【答案】3s
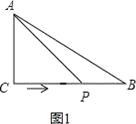
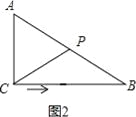
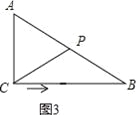
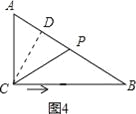
【解析】试题分析:根据题意分四种情况,针对每种情况画出相应的图形,求出相应的时间t的值即可解答本题.第一种情况:当AC=CP时,△ACP是等腰三角形,如图1所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴CP=6cm,∴t=6÷2=3秒;第二种情况:当CP=PA时,△ACP是等腰三角形,如图2所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AB=10cm,∠PAC=∠PCA,∴∠PCB=∠PBC,∴PA=PC=PB=5cm,∴t=(CB+BP)÷2=(8+5)÷2=6.5秒;第三种情况:当AC=AP时,△ACP是等腰三角形,如图3所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AP=6cm,AB=10cm,∴t=(CB+BA﹣AP)÷2=(8+10﹣6)÷2=6秒;第四种情况:当AC=CP时,△ACP是等腰三角形,如图4所示,作CD⊥AB于点D,∵∠ACB=90°,AC=6cm,BC=8cm,tan∠A=![]() ,∴
,∴![]() ,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=
,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=![]() ,∴AD=3a=
,∴AD=3a=![]() ,∴t=
,∴t=![]() =7.2s.
=7.2s.
故答案为:3,6或6.5或7.2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,四边形ABCD是平行四边形
求作:菱形AECF,使E,F分别在BC,AAD上
小凯的作法如下:
⑴连接AC
⑵作AC的垂直平分线EF分别交BC,AD于E,F
⑶连接AE,CF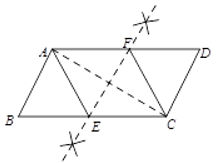
所以四边形AECF是菱形
老师说:“小凯的作法正确.”
请回答:在小凯的作法中,判定四边形AECF是菱形的依据是 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的为( )
A.锐角三角形都相似B.直角三角形都相似
C.等腰三角形都相似D.等边三角形都相似
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种说法:
(1)过直线外一点有且只有一条直线与这条直线平行;
(2)平面内,过一点能且只能作一条直线与已知直线垂直;
(3)直线外一点与直线上各点连接的所有线段中,垂线段最短;
(4)平行于同一条直线的两条直线平行.
其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→……,白甲壳虫爬行的路线是AB→BB1→……,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2015条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ).
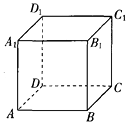
A.0 B.1 C. D.
D. 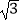
-
科目: 来源: 题型:
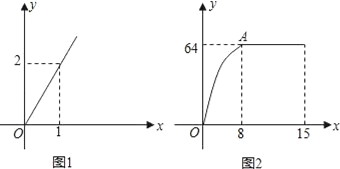
查看答案和解析>>【题目】麻城市思源实验学校自从开展“高效课堂”模式以来,在课堂上进行当堂检测效果很好.每节课40分钟教学,假设老师用于精讲的时间x(单位:分钟)与学生学习收益量y的关系如图1所示,学生用于当堂检测的时间x(单位:分钟)与学生学习收益y的关系如图2所示(其中OA是抛物线的一部分,A为抛物线的顶点),且用于当堂检测的时间不超过用于精讲的时间.
(1)求老师精讲时的学生学习收益量y与用于精讲的时间x之间的函数关系式;
(2)求学生当堂检测的学习收益量y与用于当堂检测的时间x的函数关系式;
(3)问此“高效课堂”模式如何分配精讲和当堂检测的时间,才能使学生在这40分钟的学习收益总量最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为函数
 图象上一点,连结OA,交函数
图象上一点,连结OA,交函数 的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
相关试题

