【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 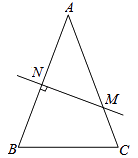
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
参考答案:
【答案】
(1)50°
(2)解:猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)=2∠B﹣90°.
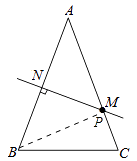
如图:
①∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是14cm,
∴AC+BC=14cm,
∴BC=6cm.
②当点P与点M重合时,PB+CP的值最小,最小值是8cm.
【解析】解:(1)若∠B=70°,则∠NMA的度数是 50°,
所以答案是:50°;
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将抛物线y=﹣2(x﹣1)2+3向下平移2个单位后所得抛物线的表达式为( )
A. y=﹣2(x+1)2+3B. y=﹣2(x﹣3)2+3
C. y=﹣2(x﹣1)2+5D. y=﹣2(x﹣1)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).
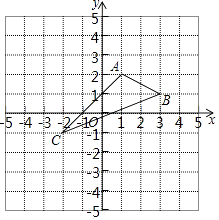
(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 .
(2)写出点A1 , B1 , C1的坐标(直接写答案)
A1
B1
C1
(3)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
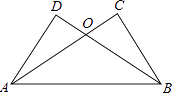
求证:
(1)BC=AD;
(2)△OAB是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】我校初三年级开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
-
科目: 来源: 题型:
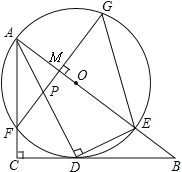
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=
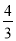 ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;(3)在(2)的条件下,求AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面哪个式子的计算结果是9﹣x2( )
A. (3﹣x)(3+x) B. (x﹣3)(x+3) C. (3﹣x)2 D. (3+x)2
相关试题

