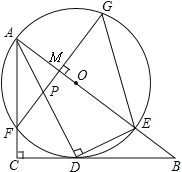
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
参考答案:
【答案】(1)证明见解析;(2)6;(3)![]()
【解析】试题分析:(1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
试题解析:(1)证明:连结OD.∵DE⊥AD,∴AE是⊙O的直径,即O在AE上.
∵AD是角平分线,∴∠1=∠2.
∵OA=OD,∴∠2=∠3.∴∠1=∠3.∴OD∥AC.
∵∠C=90°,∴OD⊥BC.∴BC是⊙O的切线.
(2)解:∵OD∥AC,∴∠4=∠EAF.
∵∠G=∠EAF,∴∠4=∠G.
∴tan∠4=tan∠G=![]() .
.
设BD=4k,则OD=OE=3k.
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+4)2,
解得,k1=2,k2=![]() (舍),(注:也可由OB=5k=3k+4得k=2),
(舍),(注:也可由OB=5k=3k+4得k=2),
∴3k=6,即⊙O的半径为6.
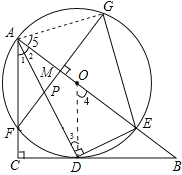
(3)解:连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=![]() ,即
,即![]() ,
, ![]() ,
,
∴![]() ,
,
∴AM=![]() AE=
AE=![]() =
=![]() .
.
∵OD∥AC,∴![]() ,
, ![]() ,即
,即![]() ,
, ![]() .
.
∴AC=![]() ,CD=
,CD=![]() .
.
∵∠1=∠2,∠ACD=∠AMP=90°,∴△ACD∽△AMP.
∴![]() ,∴PM=
,∴PM= ![]() =
=![]() .
.
∴AP=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
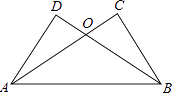
求证:
(1)BC=AD;
(2)△OAB是等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
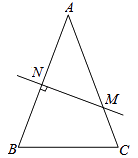
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我校初三年级开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面哪个式子的计算结果是9﹣x2( )
A. (3﹣x)(3+x) B. (x﹣3)(x+3) C. (3﹣x)2 D. (3+x)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=100°,∠2=145°,那么∠3=( )
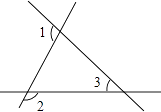
A.55°
B.65°
C.75°
D.85° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AB∥CD,直线l与直线AB、CD相交于点E、F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
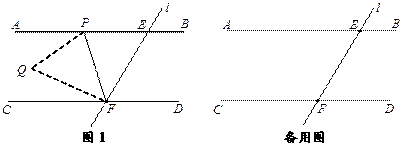
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
相关试题

