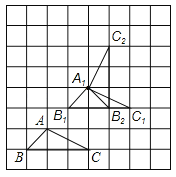
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.

参考答案:
【答案】(1)(2)作图见解析;(3)![]() .
.
【解析】
试题(1)利用平移的性质画图,即对应点都移动相同的距离.
(2)利用旋转的性质画图,对应点都旋转相同的角度.
(3)利用勾股定理和弧长公式求点B经过(1)、(2)变换的路径总长.
试题解析:解:(1)如答图,连接AA1,然后从C点作AA1的平行线且A1C1=AC,同理找到点B1,分别连接三点,△A1B1C1即为所求.
(2)如答图,分别将A1B1,A1C1绕点A1按逆时针方向旋转90°,得到B2,C2,连接B2C2,△A1B2C2即为所求.
(3)∵![]() ,
,
∴点B所走的路径总长=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B为定点,直线l∥AB,P是直线l上一动点.对于下列各值:①线段AB的长②△PAB的周长③△PAB的面积④∠APB的度数其中不会随点P的移动而变化的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请画出平移后的△A'B'C',并求△A'B'C'的面积= ;
(2)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP;
(3)请在图中画出过点C且平行于AB的直线CM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间(小时)
频数(人数)
频率
A
0≤t≤0.5
6
0.15
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
10
0.25
D
1.5≤t≤2
8
b
E
2≤t≤2.5
4
0.1
合计
1
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC.
(2)若PB=5,PH=3,求AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC和同一平面内的点D.
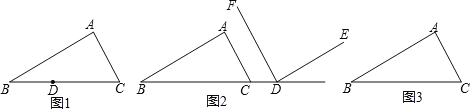
(1)如图1,点D在BC边上,过D作DE∥BA交AC于E,DF∥CA交AB于F.
①依题意,在图1中补全图形;
②判断∠EDF与∠A的数量关系,并直接写出结论(不需证明).
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A.判断DE与BA的位置关系,并证明.
(3)如图3,若点D是△ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,自己在草稿纸上试着画一画,看一看会有几种情况,然后直接写出∠EDF与∠A的数量关系(不需证明).
相关试题

