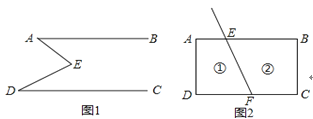
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由).
参考答案:
【答案】(1)①70°;②80°;③∠AED=∠EAB+∠EDC;(2)p点在区域①时,∠PEB+∠PFC+∠EPF=360° ;p点在区域②时,∠EPF=∠PEB+∠PFC
【解析】试题分析:(1)①根据图形猜想得出所求角度数即可;
②根据图形猜想得出所求角度数即可;
③猜想得到三角关系,理由为:延长AE与DC交于F点,由AB与DC平行,利用两直线平行内错角相等得到一对角相等,再利用外角性质及等量代换即可得证;
(2)分两个区域分别找出三个角关系即可.
试题解析:(1)①当∠A=30°,∠D=40°,则∠AED=70°
②当∠A=20°,∠D=60°,则∠AED=80°
③∠AED,∠EAB,∠EDC的关系为∠AED=∠EAB+∠EDC
证明:图1过点E作EF//AB, ∴∠AEF=∠A.
∵AB//CD, ∴EF//CD. ∴∠FED=∠D.
∴∠AED=∠AEF+∠FED=∠A+∠D.


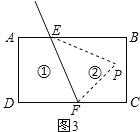
(2)图2,p点在区域①时,∠PEB+∠PFC+∠EPF=360°
图3,p点在区域②时,∠EPF=∠PEB+∠PFC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)条件下,连结BD,当∠A=32°时,求∠CBD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).
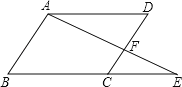
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
-
科目: 来源: 题型:
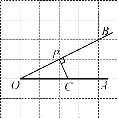
查看答案和解析>>【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C.
(1)过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到____的距离,____是点C到直线OB的距离.线段PC,PH,OC这三条线段大小关系是___.(用“<”号连接)
-
科目: 来源: 题型:
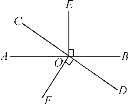
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的
 时,则
时,则  为( )
为( )
A.
B.2
C.
D.4
相关试题

