【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

参考答案:
【答案】(1)①∠BOF= 30°,∠POE=30°,②∠POE=∠BOP(2)①∠POE=∠BOP②∠POE+∠DOP=270°
【解析】
(1)①根据余角的性质得到∠BOF=∠COE=30°,求得∠COF=90°+30°=120°,根据角平分线的定义即可得到结论;
②根据垂线的性质和角平分线的定义即可得到结论;
(2)①根据角平分线的定义得到∠COP=∠POF,求得∠POE=90°+∠POF,∠BOP=90°+∠COP,于是得到∠POE=∠BOP;
②根据周角的定义即可得到结论.
(1)①∵CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE=30°,
∴∠COF=90°+30°=120°,
∵OP平分∠COF,
∴∠COP=![]() ∠COF=60°,
∠COF=60°,
∴∠POE=∠COP﹣∠COE=30°;
②CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE,
∵OP平分∠COF,
∴∠COP=∠POF,
∴∠POE=∠COP﹣∠COE,∠BOP=∠POF﹣∠BOF,
∴∠POE=∠BOP;
(2)①∵∠EOF=∠BOC=90°,
∵PO平分∠COF,
∴∠COP=∠POF,
∴∠POE=90°+∠POF,∠BOP=90°+∠COP,
∴∠POE=∠BOP;
②∵∠POE=∠BOP,∠DOP+∠BOP=270°,
∴∠POE+∠DOP=270°.
-
科目: 来源: 题型:
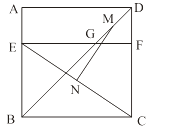
查看答案和解析>>【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
A.3
B.
C.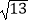
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】将两个斜边长相等的直角三角形纸片如图①放置,其中∠ACB=∠CED=90°.∠A=45°,∠D=30°.
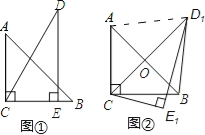
(1)∠CBA= ;
(2)把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B= .
-
科目: 来源: 题型:
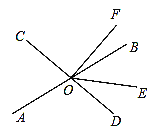
查看答案和解析>>【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°.
(1)用尺规作图作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)条件下,连结BD,当∠A=32°时,求∠CBD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠DAE=∠E,∠B=∠D.直线AD与BE平行吗?直线AB与DC平行吗?说明理由(请在下面的解答过程的空格内填空或在括号内填写理由).
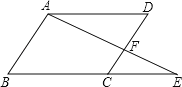
解:直线AD与BE平行,直线AB与DC .
理由如下:
∵∠DAE=∠E,(已知)
∴ ∥ ,(内错角相等,两条直线平行)
∴∠D=∠DCE. (两条直线平行,内错角相等)
又∵∠B=∠D,(已知)
∴∠B= ,(等量代换)
∴ ∥ .(同位角相等,两条直线平行)
-
科目: 来源: 题型:
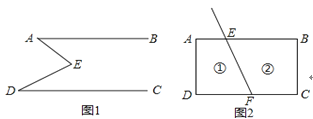
查看答案和解析>>【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:如图2,线段FE与长方形ABCD的边AB交于点E,与边CD 交于点F.图2中①②分别是被线段FE隔开的2个区域(不含边界),P是位于以上两个区域内的一点,猜想∠PEB,∠PFC,∠EPF的关系(不要求说明理由).
相关试题

