【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
参考答案:
【答案】
(1)证明:连接OB,如图所示: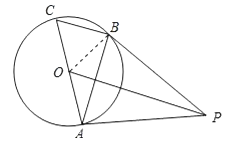
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切线
(2)解:∵⊙O的半径为2 ![]() ,
,
∴OB=2 ![]() ,AC=4
,AC=4 ![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴ ![]() ,
,
即 ![]() ,
,
∴BC=2
【解析】连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.
-
科目: 来源: 题型:
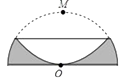
查看答案和解析>>【题目】如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线
与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线  , 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则
, 则下列结论:① a﹣b+c>0;②b>0;③阴影部分的面积为4;④若c=﹣1,则  . 其中正确的是(写出所有正确结论的序号)
. 其中正确的是(写出所有正确结论的序号)
-
科目: 来源: 题型:
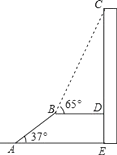
查看答案和解析>>【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈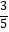 ,tan37°≈
,tan37°≈  ,sin65°≈
,sin65°≈ 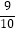 ,tan65°≈
,tan65°≈ 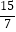 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=6,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数
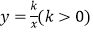 的图象与BC边交于点E.
的图象与BC边交于点E.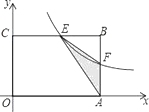
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°;在Rt△DEF中,∠EDF=90°,∠E=45°)如图①摆放,点D为AB的中点,DE交AC于点P,DF经过点C.
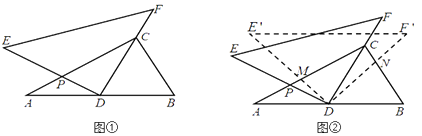
(1)求∠ADE的度数;
(2)如图②,将△DEF绕点D顺时针方向旋转角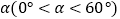 ,此时等腰直角三角尺记为
,此时等腰直角三角尺记为 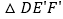 ,
, 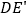 交AC于点M,
交AC于点M, 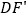 交BC于点N,试判断
交BC于点N,试判断 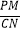 的值是否随着
的值是否随着 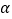 的变化而变化?如果不变,请求出
的变化而变化?如果不变,请求出 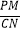 的值;反之,请说明理由.
的值;反之,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
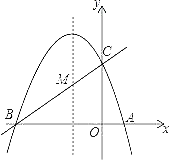
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
相关试题

