搜索
【题目】如图，在矩形OABC中，OA=6，OC=4，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数 
的图象与BC边交于点E.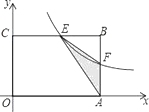
（1）当F为AB的中点时，求该函数的解析式；
（2）当k为何值时，△EFA的面积最大，最大面积是多少？
参考答案：
【答案】
（1）解：∵在矩形OABC中，OA=6，OC=4，∴B（6，4），
∵F为AB的中点，∴F（6，2），
又∵点F在反比例函数 
（k＞0）的图象上，∴k=12，
∴该函数的解析式为y= 
（x＞0）
（2）解：由题意知E，F两点坐标分别为E（ 
，4），F（6， 
），
∴ 
，
= 
= 
= 
= 
，
∴当k=12时，S有最大值．S最大=3
【解析】）当F为AB的中点时，点F的坐标为（3，1），由此代入求得函数解析式即可；根据图中的点的坐标表示出三角形的面积，得到关于k的二次函数，利用二次函数求出最值即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线
与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线 
, 则下列结论：① a﹣b+c>0；②b＞0；③阴影部分的面积为4；④若c=﹣1，则 
. 其中正确的是（写出所有正确结论的序号）
-
科目： 来源： 题型：
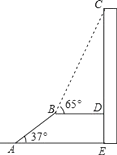
查看答案和解析>>【题目】如图，AB是长为10m，倾斜角为37°的自动扶梯，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度（结果保留整数）.
（参考数据：sin37°≈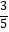
，tan37°≈ 
，sin65°≈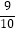 
，tan65°≈ 
）
-
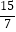科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PB、AB，∠PBA=∠C．
（1）求证：PB是⊙O的切线；
（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为2
，求BC的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C.
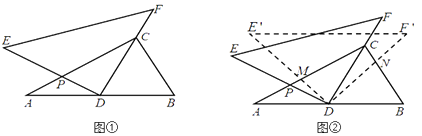
（1）求∠ADE的度数；
（2）如图②，将△DEF绕点D顺时针方向旋转角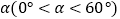
，此时等腰直角三角尺记为 
， 
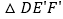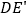交AC于点M， 
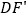交BC于点N，试判断 
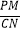的值是否随着 
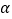的变化而变化？如果不变，请求出 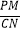的值；反之，请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
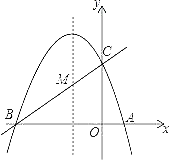
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】为调查七年级学生了解校园防欺凌知识的情况，小刚在主题班会后就本班学生对校园防欺凌知识的了解程度进行了一次调查统计：A：熟悉，B：较了解，C：知道．如下是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
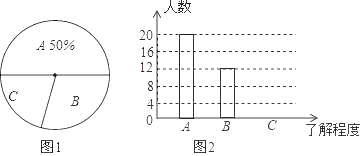
（1）求该班共有多少名学生；
（2）在条形图中将表示“知道”的部分补充完整
（3）在扇形统计图中，求“较了解”部分所对应的圆心角的度数；
（4）如果七年级共有460名同学，请你估算全年级对校园防欺凌知识“熟悉”的学生人数．
相关试题
