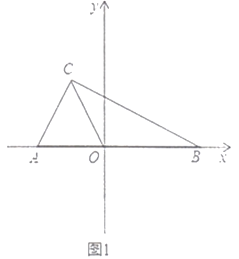
【题目】如图1,在平面直角坐标系中,![]() .
.
(1)求![]() 的面积;
的面积;
(2)点![]() 为坐标轴上一点,若
为坐标轴上一点,若![]() 的面积恰好是
的面积恰好是![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
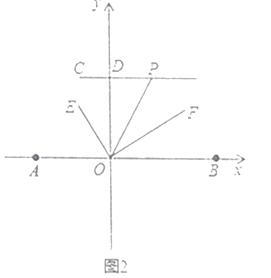
(3)如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 延长线上的一动点,连接
延长线上的一动点,连接![]() 平分
平分![]() .当点
.当点![]() 运动时,
运动时,![]() 与
与![]() 度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
参考答案:
【答案】(1)5;(2)![]() 或
或![]() (0,5)或(0,-5);(3)
(0,5)或(0,-5);(3)![]() 与
与![]() 度数之间的数量关系不变,
度数之间的数量关系不变,![]() .
.
【解析】
(1)根据三角形的面积公式计算即可.
(2)分两种情形分别构建方程即可解决问题.
(3)根据平行线的性质及证明∠1=∠3即可解决问题.
![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,重足为
轴,重足为![]()
![]() ,
,
![]() ,
,
![]()
![]() ;
;

![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]()
![]()
![]()
由![]() 知
知![]() ,
,
![]()
①当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
②当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
点![]() 的坐标为
的坐标为![]() 或
或![]()
(3)结论:∠OPD=2∠DOE.
理由:如图2,
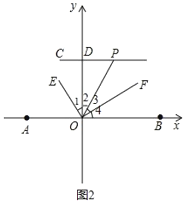
∵OE平分∠AOP,
∴∠AOE=∠POE=∠1+∠2,
∵OF⊥OE,
∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,
∴∠3=∠4,
∵CD⊥y轴,
∴CD∥AB,
∴∠OPD=∠POB=2∠3,
∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,
∴∠1+∠2+∠3=∠2+2∠3,
∴∠1=∠3,
由∠DOE=∠1,∠OPD=∠POB=2∠1
∴∠OPD=2∠DOE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 分别为长方形
分别为长方形 的边
的边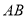 和边
和边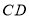 上的一个动点,将四边形
上的一个动点,将四边形 沿直线
沿直线 折叠,点
折叠,点 恰好落在
恰好落在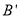 处,若
处,若 ,则此时
,则此时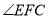 的度数为____.
的度数为____.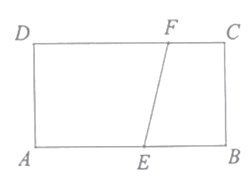
-
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
垃圾桶
15
鞋架
40
字画
a
2
90
合计
5
185
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图,不写作法,保留作图痕迹.
如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AB、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=15°,求∠BPC的度数.
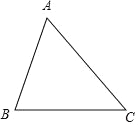
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A.
 B.
B.  C.
C. 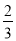 D.
D. 
相关试题

