【题目】如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为 . 
参考答案:
【答案】5
【解析】解:∵四边形ABCD是正方形,AC为对角线,
∴∠EAF=45°,
又∵EF⊥AC,
∴∠AFE=90°,∠AEF=45°,
∴EF=AF=3,
∵△EFC的周长为12,
∴FC=12﹣3﹣EC=9﹣EC,
在Rt△EFC中,EC2=EF2+FC2,
∴EC2=9+(9﹣EC)2,
解得EC=5.
所以答案是:5.
【考点精析】本题主要考查了等腰直角三角形和勾股定理的概念的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】新房装修后,某居民购买家用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称
单价(元)
数量(个)
金额(元)
垃圾桶
15
鞋架
40
字画
a
2
90
合计
5
185
(1)居民购买垃圾桶,鞋架各几个?
(2)若居民再次购买字画和垃圾桶两种家居用品共花费150元,则有哪几种不同的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
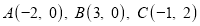 .
.(1)求
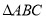 的面积;
的面积;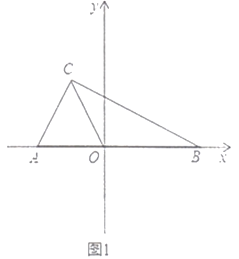
(2)点
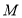 为坐标轴上一点,若
为坐标轴上一点,若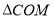 的面积恰好是
的面积恰好是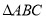 面积的一半,求点
面积的一半,求点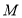 的坐标.
的坐标.(3)如图2,过点
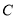 作
作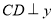 轴于点
轴于点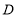 ,点
,点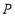 为
为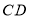 延长线上的一动点,连接
延长线上的一动点,连接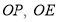 平分
平分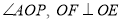 .当点
.当点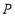 运动时,
运动时,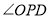 与
与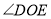 度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.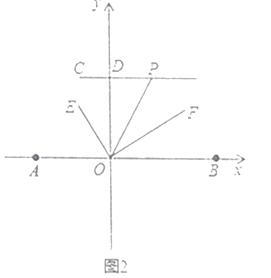
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图,不写作法,保留作图痕迹.
如图,△ABC中,∠A=60°.
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到AB、BC两边的距离也相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=15°,求∠BPC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

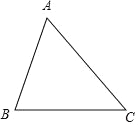
A.
 B.
B.  C.
C. 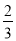 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:(-1)3-
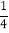 ×[2-(-3)2]
×[2-(-3)2](2) 计算:(﹣12)+(+30)﹣(+65)﹣(﹣47)
(3) 计算:39
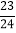 ×(﹣12)
×(﹣12)(4) 计算:(﹣1000)×(
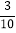 ﹣
﹣ +
+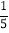 ﹣0.1)
﹣0.1)(5)化简:﹣4(a3﹣3b)+(﹣2b2+5a3)
(6)化简:2a﹣2(﹣0.5a+3b﹣c)
-
科目: 来源: 题型:
查看答案和解析>>【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克)
30
35
40
45
50
日销售量p(千克)
600
450
300
150
0
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
相关试题

