【题目】二次函数![]() 图象
图象![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象![]() 轴下方的部分组成一个“
轴下方的部分组成一个“![]() ”形状的新图象,若直线
”形状的新图象,若直线![]() 与该新图象有两个公共点,则
与该新图象有两个公共点,则![]() 的取值范围为_____.
的取值范围为_____.
参考答案:
【答案】![]() 或
或![]()
【解析】
画出图象求出直线经过点A和原点时的b的值,结合图象可以确定b的范围,再求出直线与翻折后的抛物线只有一个交点时的b的值,可以利用方程组只有一组解△=0解决问题,由此再确定b的取值范围.
如图,
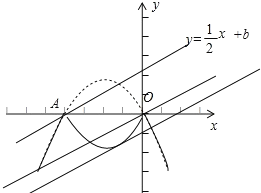
当直线![]() 经过点A(2,0)时,b=1,
经过点A(2,0)时,b=1,
当直线![]() 经过点O(0,0)时,b=0,
经过点O(0,0)时,b=0,
∴0<b<1时,直线![]() 与新图形有两个交点,
与新图形有两个交点,
翻折后的抛物线为![]()
由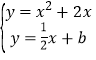 方程组有一组解,消去y得到:2x2+3x2b=0,
方程组有一组解,消去y得到:2x2+3x2b=0,
∵△=0,
∴9+16b=0,
![]()
由图象可知,![]() 时,直线
时,直线![]() 与新图形有两个交点.
与新图形有两个交点.
综上所述0<b<1或![]() 时,直线
时,直线![]() 与新图形有两个交点.
与新图形有两个交点.
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
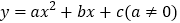 的图象如图所示,现有下列结论:①
的图象如图所示,现有下列结论:①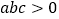 ;②
;② ;③
;③ ;④
;④ .则其中结论正确的是( )
.则其中结论正确的是( )
A. ①③ B. ③④ C. ②③ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
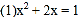
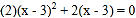
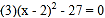
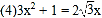 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是关于
是关于 的二次函数.求:
的二次函数.求: 满足条件的
满足条件的 的值;
的值; 为何值时,抛物线有最低点?求出这个最低点,这时当
为何值时,抛物线有最低点?求出这个最低点,这时当 为何值时,
为何值时, 随
随 的增大而增大?
的增大而增大? 为何值时,函数有最大值?最大值是多少?这时当
为何值时,函数有最大值?最大值是多少?这时当 为何值时,
为何值时, 随
随 的增大而减小?
的增大而减小? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点
 ,以
,以 为直径在第一象限内作半圆,
为直径在第一象限内作半圆, 为半圆上一点,连接
为半圆上一点,连接 并延长至
并延长至 ,使
,使 ,过
,过 作
作 轴于点
轴于点 ,交线段
,交线段 于点
于点 ,已知
,已知 ,抛物线经过
,抛物线经过 、
、 、
、 三点.
三点.
 ________°.
________°. 求抛物线的函数表达式.
求抛物线的函数表达式. 若
若 为抛物线上位于第一象限内的一个动点,以
为抛物线上位于第一象限内的一个动点,以 、
、 、
、 、
、 为顶点的四边形面积记作
为顶点的四边形面积记作 ,则
,则 取何值时,相应的点
取何值时,相应的点 有且只有
有且只有 个?
个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个长为
 米的篱笆,一面利用墙(墙的最大长度
米的篱笆,一面利用墙(墙的最大长度 为
为 米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽
米)围成的中间隔有一道篱笆的长方形花圃.设花圃的宽 为
为 米,面积为
米,面积为 平方米.
平方米.
 求
求 与
与 的函数关系式;
的函数关系式; 如果要围成花圃的面积为
如果要围成花圃的面积为 平方米,求
平方米,求 的长为多少米?
的长为多少米? 如果要使围成花圃面积最大,求
如果要使围成花圃面积最大,求 的长为多少米?
的长为多少米?
相关试题

