【题目】如图,已知D是BC的中点,过点D作BC的垂线交∠BAC的平分线于点E,EF⊥AB于点F,EG⊥AC于点G.
(1)求证:BF=CG;
(2)若AB=10,AC=6,求线段CG的长.

参考答案:
【答案】(1)证明见解析;(2)CG=2.
【解析】
本题需先连接EC、EB,根据AE是∠CAB的平分线,得出EG=EF,再根据ED垂直平分BC,得出Rt△CGE≌Rt△BFE,从而证出BF=CG;
本题根据AE是∠CAB的平分线,得出∠FAE=∠GAE,再根据EF⊥AB于点F,EG⊥AC于点G,得出∠AFE=∠AGE ,即可证得△AFE≌△AGE ,从而得到AF=AG,
设BF=CG=x, AG=AF=y,组成二元一次方程组即可求解.
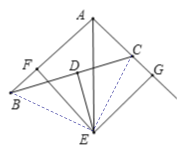
(1)连接EC、EB
![]() AE是∠CAB的平分线,
AE是∠CAB的平分线,
EF⊥AB于点F,EG⊥AC于点G,
![]() EG=EF
EG=EF
![]() 点D是BC的中点,ED垂直BC
点D是BC的中点,ED垂直BC
∴ED垂直平分BC,
![]() EC=EB
EC=EB
![]() Rt△CGE≌Rt△BFE(HL),
Rt△CGE≌Rt△BFE(HL),
![]() BF=CG
BF=CG
(2)![]() AE是∠CAB的平分线
AE是∠CAB的平分线
∴∠FAE=∠GAE
∵EF⊥AB于点F,EG⊥AC
∴∠AFE=∠AGE=90°
在△AFE和△AGE中
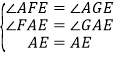 ,
,
∴△AFE≌△AGE(AAS)
∴AF=AG
设BF=CG=x, AG=AF=y
∴AB=AF+BF=x+y=10
AC=AG-CG=y-x=6
∴![]()
解得![]()
∴CG=BF=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
-
科目: 来源: 题型:
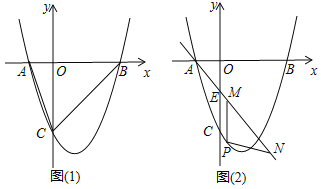
查看答案和解析>>【题目】如图(1),抛物线
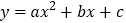 与x轴交于A(1,0)、B(t,0)(t >0)两点,与y轴交于点C(0,3),若抛物线的对称轴为直线x=1,
与x轴交于A(1,0)、B(t,0)(t >0)两点,与y轴交于点C(0,3),若抛物线的对称轴为直线x=1, (1)求抛物线的函数解析式;
(2 若点D是抛物线BC段上的动点,且点D到直线BC的距离为
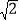 ,求点D的坐标
,求点D的坐标(3)如图(2),若直线y=mx+n经过点A,交y轴于点E(0,1),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
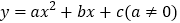 的图象如图所示,现有下列结论:①
的图象如图所示,现有下列结论:①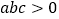 ;②
;② ;③
;③ ;④
;④ .则其中结论正确的是( )
.则其中结论正确的是( )
A. ①③ B. ③④ C. ②③ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
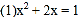
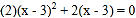
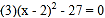
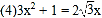 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
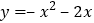 图象
图象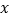 轴上方的部分沿
轴上方的部分沿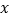 轴翻折到
轴翻折到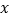 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象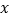 轴下方的部分组成一个“
轴下方的部分组成一个“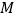 ”形状的新图象,若直线
”形状的新图象,若直线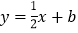 与该新图象有两个公共点,则
与该新图象有两个公共点,则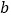 的取值范围为_____.
的取值范围为_____.
相关试题

