【题目】下列叙述:
①最小的正整数是![]() ;
;
②若![]() 是一个负数,则
是一个负数,则![]() 一定是负数;
一定是负数;
③用一个平面去截正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
其中正确的个数有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
整数包括正整数、0、负整数,可对①进行判别;解不等式即可对②进行判别;根据用一个平面去截正方体的性质可对③进行判别;根据多边形的概念可对④进行判别;根据绝对值的概念可对⑤进行判别.
①最小的正整数是1,故错误;
②![]() ,解得:
,解得:![]() ,所以
,所以![]() 一定是负数,故正确;
一定是负数,故正确;
③用一个平面去截正方体,截面与六个面都相交即可得六边形,故错误;
④三角形是多边形,故正确;
⑤绝对值等于本身的数是正整数和0,故错误.
综上:正确的个数有2个,
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位急需用车,但又不准备买车,他们准备和一个体车主或一国营出租车公司其中的一家签订月租车合同.设汽车每月行驶xkm,应付给个体车主的月租费用是y1元,应付给出租公司的月租费用是y2元,y1、y2分别与x之间的函数关系图像(两条射线)如图所示,观察图像回答下列问题:
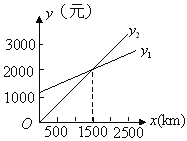
(1)每月行驶的路程在什么范围内时,租国有公司的车合算?
(2)每月行驶的路程等于多少时,租两家车的费用相同?
(3)如果这个单位估计每月行驶的路程为2300km,那么这个单位租哪家的车合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一艘轮船和一艘快艇沿相同的路线从甲港出发驶向乙港的过程中,路程
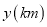 随时间
随时间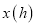 变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题:
变化的图像如图示(分别是正比例函数的图像和一次函数的图像).根据图中提供的信息解答下列问题: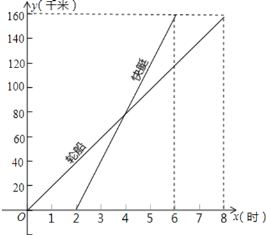
(1)分别求出表示轮船和快艇行驶过程中路程
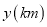 和时间
和时间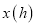 之间的函数解析式(不要求写出自变量的取值范围);
之间的函数解析式(不要求写出自变量的取值范围);(2)轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
(3)快艇出发多长时间赶上轮船?
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线
 上点
上点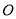 为端点作射线
为端点作射线 ,使
,使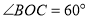 ,将直角
,将直角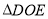 的直角顶点放在点
的直角顶点放在点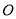 处.
处.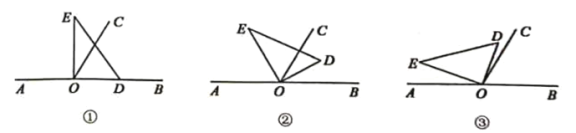
(1)若直角
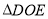 的边
的边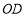 在射线
在射线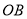 上(图①),求
上(图①),求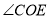 的度数;
的度数;(2)将直角
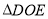 绕点
绕点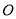 按逆时针方向转动,使得
按逆时针方向转动,使得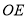 所在射线平分
所在射线平分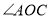 (图②),说明
(图②),说明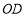 所在射线是
所在射线是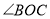 的平分线;
的平分线;(3)将直角
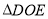 绕点
绕点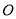 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得 (图③),求
(图③),求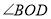 的度数.
的度数. -
科目: 来源: 题型:
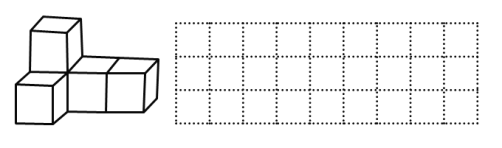
查看答案和解析>>【题目】下图是由大小相同的小立方体搭乘的几何体:
(1)请在所给的方格中画出该几何体从上面看和从左面看的两个图形;
(2)现在你的手里还有一些相同的小立方块,如果保持从上面来看和从左面看所得到的图形不变,则在左边的立体图形中最多可以添加 个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
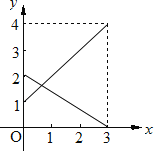
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°,∠B'=110°,∠BCA'的度数是( )
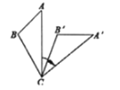
A.110°B.80°C.40°D.30°
相关试题

