【题目】某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
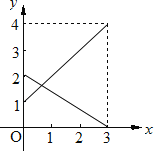
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
参考答案:
【答案】(1)甲:y=-![]() x+2 乙:y=x+1 (2)x=0.6 (3)1小时.
x+2 乙:y=x+1 (2)x=0.6 (3)1小时.
【解析】
(1)利用待定系数法进行求解;
(2)当y相等时列出x的方程,然后进行求解;
(3)分别设两个蓄水池的底面积,然后根据体积相等进行求解.
(1)甲蓄水池中水的深度y与注水时间x之间的函数关系式为:y=-![]() x+2
x+2
乙蓄水池中水的深度y与注水时间x之间的函数关系式为:y=x+1
(2) 当-![]() x+2=x+1时, 解得:x=0.6;
x+2=x+1时, 解得:x=0.6;
(3)设甲蓄水池的底面积为![]() ,乙蓄水池的底面积为
,乙蓄水池的底面积为![]() ,t小时甲、乙两个蓄水池的蓄水量相同.
,t小时甲、乙两个蓄水池的蓄水量相同.
∵甲水深度下降2米,而乙水池深度升高3米,所以甲乙两水池的底面积比是3:2,
∴2![]() =3×6, ∴S1=9, ∵(4-1)
=3×6, ∴S1=9, ∵(4-1)![]() =3×6, ∴
=3×6, ∴![]() =6,
=6,
∵![]() (-
(-![]() x+2)=
x+2)=![]() (t+1) 解得t=1.
(t+1) 解得t=1.
∴注水1小时甲、乙两个蓄水池的蓄水量相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以直线
 上点
上点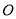 为端点作射线
为端点作射线 ,使
,使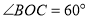 ,将直角
,将直角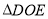 的直角顶点放在点
的直角顶点放在点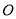 处.
处.
(1)若直角
 的边
的边 在射线
在射线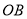 上(图①),求
上(图①),求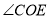 的度数;
的度数;(2)将直角
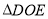 绕点
绕点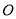 按逆时针方向转动,使得
按逆时针方向转动,使得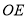 所在射线平分
所在射线平分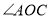 (图②),说明
(图②),说明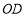 所在射线是
所在射线是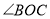 的平分线;
的平分线;(3)将直角
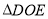 绕点
绕点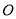 按逆时针方向转动到某个位置时,恰好使得
按逆时针方向转动到某个位置时,恰好使得 (图③),求
(图③),求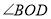 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列叙述:
①最小的正整数是
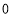 ;
;②若
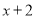 是一个负数,则
是一个负数,则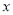 一定是负数;
一定是负数;③用一个平面去截正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
其中正确的个数有( )
A.
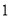 B.
B.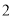 C.
C.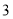 D.
D.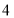
-
科目: 来源: 题型:
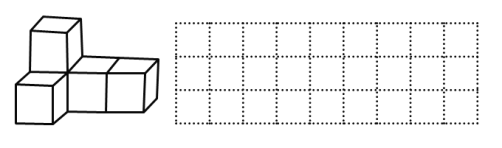
查看答案和解析>>【题目】下图是由大小相同的小立方体搭乘的几何体:
(1)请在所给的方格中画出该几何体从上面看和从左面看的两个图形;
(2)现在你的手里还有一些相同的小立方块,如果保持从上面来看和从左面看所得到的图形不变,则在左边的立体图形中最多可以添加 个小立方块.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°,∠B'=110°,∠BCA'的度数是( )
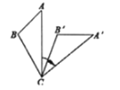
A.110°B.80°C.40°D.30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO
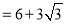 ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=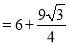 .其中正确的结论是( )
.其中正确的结论是( )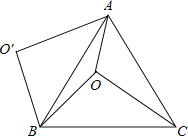
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 年
年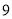 月
月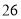 日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:(1)本次调查共调查了 人,“比较了解”所占扇形统计图圆心角的度数为 ;
(2)请将两个统计图补充完整;
(3)若玲玲所在的学校有
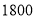 人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
人,请你估计一下“非常了解”和“比较了解”大约共有多少人?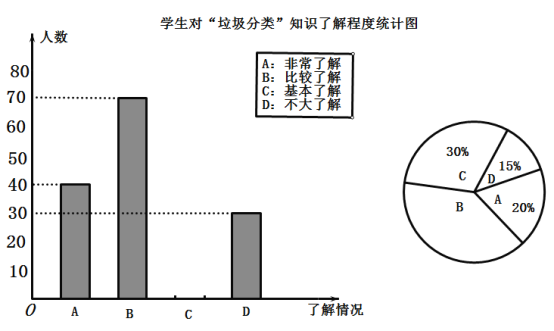
相关试题

