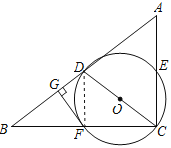
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与⊙O的位置关系,并说明理由.
(2)若AC=3,CD=2.5,求FG的长.

参考答案:
【答案】(1)FG与⊙O相切,理由见解析;(2)FG=![]() .
.
【解析】
(1)如图,连接OF,根据直角三角形斜边中线的性质可得CD=BD,即可得到∠DBC=∠DCB,根据等腰三角形的性质得到∠OFC=∠OCF,可得∠OFC=∠DBC,即可证明OF//DB,根据平行线的性质可推出∠OFG=90°,即可得到结论;
(2)连接DF,根据勾股定理得到BC=![]() =4,根据圆周角定理得到∠DFC=90°,根据等腰三角形“三线合一”的性质可得BF=
=4,根据圆周角定理得到∠DFC=90°,根据等腰三角形“三线合一”的性质可得BF=![]() BC=2,根据三角函数的定义即可得到结论.
BC=2,根据三角函数的定义即可得到结论.
(1)FG与⊙O相切,
理由:如图,连接OF,
∵∠ACB=90°,D为AB的中点,
∴CD=BD,
∴∠DBC=∠DCB,
∵OF=OC,
∴∠OFC=∠OCF,
∴∠OFC=∠DBC,
∴OF∥DB,
∴∠OFG+∠DGF=180°,
∵FG⊥AB,
∴∠DGF=90°,
∴∠OFG=90°,
∴FG与⊙O相切.
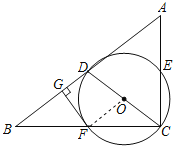
(2)连接DF,
∵CD=2.5,
∴AB=2CD=5,
∵AC=3,
∴BC=![]() =4,
=4,
∵CD为⊙O的直径,
∴∠DFC=90°,
∴FD⊥BC,
∵DB=DC,
∴BF=![]() BC=2,
BC=2,
∵sin∠ABC=![]() ,
,
即![]() ,
,
∴FG=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中,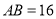 ,
, ,点
,点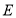 、
、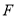 分别在边
分别在边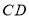 、
、 上.
上.(1)若
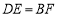 ,求证:四边形
,求证:四边形 是平行四边形;
是平行四边形;(2)若四边形
 是菱形,求菱形
是菱形,求菱形 的周长.
的周长.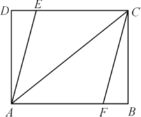
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店专售一款电动牙刷,其成本为 20 元/支,销售中发现该商品每天的销售量
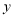 (支)与销售单价
(支)与销售单价 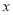 (元/支)之间存在如图所示的关系.
(元/支)之间存在如图所示的关系. (1)求出
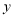 与
与 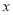 的函数关系式(不需要写出自变量取值范围);
的函数关系式(不需要写出自变量取值范围); (2)该款电动牙刷销售单价定为多少元时,每天销售利润最大?最大利润是多少元?
(3)近期武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出 200元捐赠给武汉,为了保证捐款后每天剩余利润不低于 550 元,试确定该款电动牙刷销售单价
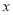 的取值范围?
的取值范围?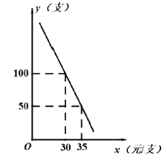
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC=20,tanB=
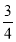 ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
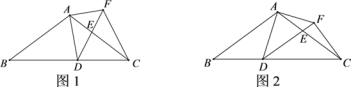
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=|a|x2+bx+c的图象经过A(m,n)、B(0,y1)、C(3-m,n)、D(
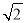 , y2)、E(2,y3),则y1、y2、y3的大小关系是( ).
, y2)、E(2,y3),则y1、y2、y3的大小关系是( ).A. y1< y2< y3B. y1 < y3< y2C. y3< y2< y1D. y2< y3< y1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=4﹣x与双曲线y
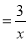 交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA为直径的圆与直线BC的交点坐标是_____.
相关试题

