搜索
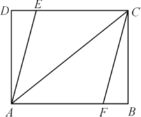
【题目】如图，在矩形
中，
，
，点
、
分别在边
、
上．
（1）若
，求证：四边形
是平行四边形；
（2）若四边形是菱形，求菱形的周长．
参考答案：
【答案】（1）详见解析；（2）50
【解析】
（1）首先根据矩形的性质可得AB∥CD且AB=CD，然后根据DE=BF，可得AF∥CE，AF=CE即可证明四边形AFCE是平行四边形；
（2）根据四边形AFCE是菱形，可得AE=CE，然后设AE=CE=x，表示出DE的长度，根据勾股定理得到关于x的方程求出x的值，继而可求得菱形的边长及周长.
（1）证明：∵四边形
为矩形
∴
，
∴
∵
，
，
∴
∵
∴四边形AFCE是平行四边形．
（2）解：∵四边形
是菱形
∴
∵，
∴
设
，则
∵四边形ABCD是矩形
∴
∴在
中，
又∵
，
∴
，解得
∴
答：菱形的周长为50．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC 的顶点分别为 A（-2，2）、B（-4，5）、C（-5，1）和直线 m （直线 m 上各点的横坐标都为 1）．
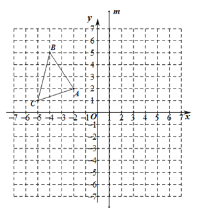
（1）作出△ABC 关于
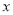轴对称的图形△A1B1C1，并写出点 A1 的坐标；（2）作出点 C关于直线 m 对称的点C2 ， 并写出点C2 的坐标；
（3）在
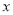轴上找一点P，使 PA+PC的值最小，请直接写出点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性，中国移动支付在世界处于领先水平．为了解人们平时最喜欢用哪种移动支付方式，因此在某步行街对行人进行随机抽样调查，以下是根据调查结果分别整理的不完整的统计表和统计图．
移动支付方式
支付宝
微信
其他
人数/人
200
75
请你根据上述统计表和统计图提供的信息．完成下列问题：
（1）在此次调查中，使用支付宝支付的人数；
（2）求表示微信支付的扇形所对的圆心角度数；
（3）某天该步行街人流量为10万人，其中30%的人购物并选择移动支付，请你依据此次调查获得的信息估计一下当天使用微信支付的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在歌唱比赛中，一位歌手分别转动如下的两个转盘（每个转盘都被分成3等份）一次，根据指针指向的歌曲名演唱两首曲目．
（1）转动转盘①时，该转盘指针指向歌曲“3”的概率是 ；
（2）若允许该歌手替换他最不擅长的歌曲“3”，即指针指向歌曲“3”时，该歌手就选择自己最擅长的歌曲“1”， 请用树形图或列表法中的一种，求他演唱歌曲“1”和“4”的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某网店专售一款电动牙刷，其成本为 20 元/支，销售中发现该商品每天的销售量
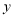（支）与销售单价 
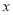（元/支）之间存在如图所示的关系． （1）求出
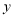与 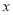的函数关系式（不需要写出自变量取值范围）； （2）该款电动牙刷销售单价定为多少元时，每天销售利润最大?最大利润是多少元?
（3）近期武汉爆发了“新型冠状病毒”疫情，该网店店主决定从每天获得的利润中抽出 200元捐赠给武汉，为了保证捐款后每天剩余利润不低于 550 元，试确定该款电动牙刷销售单价
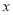的取值范围？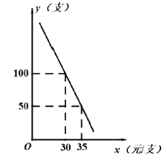
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．
（1）试判断FG与⊙O的位置关系，并说明理由．
（2）若AC＝3，CD＝2.5，求FG的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，AB＝AC＝20，tanB＝
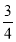，点D为BC边上的动点（D不与点B，C重合）．以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF⊥AD交射线DE于点F，连接CF．（1）求证：△ABD∽△DCE；
（2）当DE∥AB时（如图2），求AE的长；
（3）点D在BC边上运动的过程中，是否存在某个位置，使得DF＝CF？若存在，求出此时BD的长；若不存在，请说明理由．
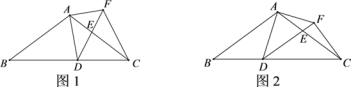
相关试题
