【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=70°,∠C=30°,求∠DAE和∠AOB.

参考答案:
【答案】20°,105°.
【解析】
先根据三角形内角和定理计算出∠BAC=180°-∠ABC-∠C=80°,再根据角平分线的性质得到∠CAE=![]() ∠BAC=40°,利用三角形外角性质得∠AED=∠CAE+∠C=70°,进一步求得∠DAE;
∠BAC=40°,利用三角形外角性质得∠AED=∠CAE+∠C=70°,进一步求得∠DAE;
利用三角形外角的性质得出∠AOB=∠AED+∠CBF进行计算.
∵∠ABC=70°,∠C=30°,
∴∠BAC=180°﹣∠ABC﹣∠C=80°,
∵AE、BF分别是∠BAC、∠ABC的平分线,
∴∠CAE=![]() ∠BAC=40°,∠CBF=
∠BAC=40°,∠CBF=![]() ∠ABC=35°,
∠ABC=35°,
∴∠AED=∠CAE+∠C=40°+30°=70°,
∵AD⊥BC,
∴∠DAE=90°﹣∠AED=20°;
∵∠AOB=∠AED+∠CBF,
∴∠AOB=70°+35°=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,CD、CE分别是△ABC的高和角平分线,∠BAC=α,∠B=β(α>β).

(1)若α=70°,β=40°,求∠DCE的度数;
(2)试用α、β的代数式表示∠DCE的度数(直接写出结果);
(3)如图②,若CE是△ABC外角∠ACF的平分线,交BA延长线于点E,且α﹣β=30°,求∠DCE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=∠C,D,E,F分别是BC,AC,AB上的点,且BF=CD,BD=CE,∠FDE=55°,则∠A=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一条高与一腰的夹角为40°,则等腰三角形的一个底角为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC 中,AB=AC=12 厘米,∠B=∠C,BC=8 厘米,点 D 为 AB 的中点.如果点 P 在线段 BC 上以 2 厘米/秒 的速度由 B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C 点向 A 点运动.若点 Q 的运动速度为 v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( )

A.2B.5C.1 或 5D.2 或 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=
 .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.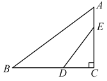
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=BC,∠ABC=90°,F 为 AB 延长线上一点,点 E 在BC 上,且 AE=CF.

(1)求证: AE⊥CF;
(2)若∠CAE=25°,求∠ACF 的度数.
相关试题

