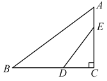
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
参考答案:
【答案】![]()
【解析】
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,根据折叠的性质得到DE⊥CF,OC=OF,再根据等角的余角相等得∠1=∠EDC,而∠EDC=∠A,则∠1=∠A,所以FC=FA,同理可得FC=FB,于是有CF=![]() AB,OC=
AB,OC=![]() AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=
AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=![]() ,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=
,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=![]() ,OD=
,OD=![]() ,再计算OE+OD即可.
,再计算OE+OD即可.
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,如图,

∴DE⊥CF,OC=OF,
∵∠EDC+∠OCD=90°,∠1+∠OCD=90°,
∴∠1=∠EDC,
而∠EDC=∠A,
∴∠1=∠A,
∴FC=FA,
同理可得FC=FB,
∴CF=![]() AB,
AB,
∴OC=![]() AB,
AB,
在Rt△ABC中,∠C=90°,AC=3,
∴tanA=![]() ,
,
∴BC=4,
∴AB=![]() =5,
=5,
∴OC=![]() ,
,
在Rt△OEC中,tan∠1=tan∠A=![]() ,
,
∴OE=![]() ,
,
在Rt△ODC中,tan∠ODC=tan∠A=![]() ,
,
∴OD=![]() ,
,
∴DE=OD+OE=![]() +
+![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一条高与一腰的夹角为40°,则等腰三角形的一个底角为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠ABC=70°,∠C=30°,求∠DAE和∠AOB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC 中,AB=AC=12 厘米,∠B=∠C,BC=8 厘米,点 D 为 AB 的中点.如果点 P 在线段 BC 上以 2 厘米/秒 的速度由 B 点向 C 点运动,同时,点 Q 在线段 CA 上由 C 点向 A 点运动.若点 Q 的运动速度为 v 厘米/秒,则当△BPD 与△CQP 全等时,v 的值为( )

A.2B.5C.1 或 5D.2 或 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 中,AB=BC,∠ABC=90°,F 为 AB 延长线上一点,点 E 在BC 上,且 AE=CF.

(1)求证: AE⊥CF;
(2)若∠CAE=25°,求∠ACF 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下面例题,解答问题:例题: 已知二次三项式x2 4x m 有一个因式是 ( x 3) ,求另一个因式以及 m 的值.
解:设另一个因式为 ( x n) ,得x2 4x m ( x 3) ( x n)
则x2 4 x m x2 (n 3) x 3n
∴

解得: n 7, m 21
∴ 另一个因式为 ( x 7) , m 的值为-21 .
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值.
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列各题:
(1)先化简,再求代数式(
 的值,其中x=
的值,其中x= cos30°+
cos30°+ ;
;(2)已知α是锐角,且sin(α+15°)=
 .计算
.计算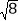 -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+( )-1的值.
)-1的值.
相关试题

