Question

【题目】如图①，在△ABC中，CD、CE分别是△ABC的高和角平分线，∠BAC＝α，∠B＝β（α＞β）．

（1）若α＝70°，β＝40°，求∠DCE的度数；

（2）试用α、β的代数式表示∠DCE的度数（直接写出结果）；

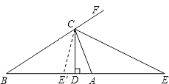
（3）如图②，若CE是△ABC外角∠ACF的平分线，交BA延长线于点E，且α﹣β＝30°，求∠DCE的度数．

Answer 1

【答案】（1）15°；（2）；（3）75°．

【解析】

（1）三角形的内角和是180°，已知∠BAC与∠ABC的度数，则可求出∠BAC的度数，然后根据角平分线的性质求出∠BCE，再利用三角形的一个外角等于和它不相邻的两个内角的和求出∠DEC的度数，进而求出∠DCE的度数；
（2）∠DCE＝ ．
（3）作∠ACB的内角平分线CE′，根据角平分线的性质求出∠ECE′=∠ACE+∠ACE′=∠ACB+∠ACF=90°，进而求出∠DCE的度数．

解：（1）因为∠ACB＝180°﹣（∠BAC+∠B）＝180°﹣（70°+40°）＝70°，

又因为CE是∠ACB的平分线，

所以．

因为CD是高线，

所以∠ADC＝90°，

所以∠ACD＝90°﹣∠BAC＝20°，

所以∠DCE＝∠ACE﹣∠ACD＝35°﹣20°＝15°．

（2）．

（3）如图，作∠ACB的内角平分线CE′，

则．

因为CE是∠ACB的外角平分线，

所以∠ECE′＝∠ACE+∠ACE′＝＝＝90°，

所以∠DCE＝90°﹣∠DCE′＝90°﹣15°＝75°．

即∠DCE的度数为75°．