【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)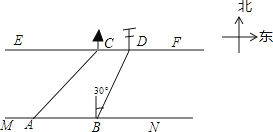
参考答案:
【答案】30+10 ![]()
【解析】解:如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,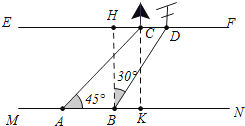
设CK=HB=x,
∵∠CKA=90°,∠CAK=45°,
∴∠CAK=∠ACK=45°,
∴AK=CK=x,BK=HC=AK﹣AB=x﹣30,
∴HD=x﹣30+10=x﹣20,
在RT△BHD中,∵∠BHD=30°,∠HBD=30°,
∴tan30°= ![]() ,∴
,∴ ![]() =
= ![]() ,解得x=30+10
,解得x=30+10 ![]() .
.
∴河的宽度为(30+10 ![]() )米.
)米.
如图作BH⊥EF,CK⊥MN,垂足分别为H、K,则四边形BHCK是矩形,设CK=HB=x,根据tan30°= ![]() 列出方程即可解决问题.本题考查解直角三角形的应用、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用三角函数的定义,列出方程解决问题,属于中考常考题型.
列出方程即可解决问题.本题考查解直角三角形的应用、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用三角函数的定义,列出方程解决问题,属于中考常考题型.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为 .
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB=2
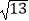 cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长cm.
cm,AD=4cm,AC⊥BC,则△DBC比△ABC的周长长cm.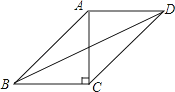
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,△ABD、△BCE均为等边三角形,DE、AB交于点F,AF=3
 ,则△ACE的面积为_____.
,则△ACE的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的二次函数y=ax2+bx+c的图象经过点(﹣2,y1),(﹣1,y2),(1,0),且y1<0<y2 , 对于以下结论:
①abc>0;②a+3b+2c≤0;③对于自变量x的任意一个取值,都有 x2+x≥﹣
x2+x≥﹣ 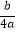 ;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣
;④在﹣2<x<﹣1中存在一个实数x0 , 使得x0=﹣ 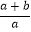 ,
,
其中结论错误的是 (只填写序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列不等式(组):
(1)x-
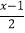 <2-
<2-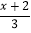 .
.(2)-2≤
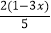 ≤7
≤7(3)
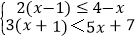 ;
;(4)
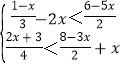
相关试题

