搜索
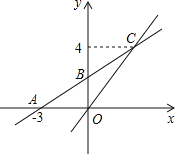
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交点为A（-3，0），与y轴交点为B，且与正比例函数
的图象的交于点C（m，4）．
（1）求m的值及一次函数y=kx+b的表达式；
（2）若点P是y轴上一点，且△BPC的面积为6，请直接写出点P的坐标．
参考答案：
【答案】（1）m的值为3，一次函数的表达式为
（2） 点P 的坐标为（0， 6）、（0，－2）
【解析】
（1）首先利用待定系数法把C（m，4）代入正比例函数y=
x中，计算出m的值，进而得到C点坐标，再利用待定系数法A、C两点坐标代入一次函数y=kx+b中，计算出k、b的值进而得到一次函数解析式.
（2）利用△BPC的面积为6，即可得出点P的坐标.
解：（1）∵ 点C（m，4）在正比例函数
的图象上，
∴ 
·m， 
即点C坐标为（3，4）
∵ 一次函数 
经过A（－3，0）、点C（3，4）
∴ 
解得：
∴ 一次函数的表达式为
（2） 点P 的坐标为（0， 6）、（0，－2）
“点睛”此题主要考查了待定系数法求一次函数解析式知识，根据待定系数法把A、C两点坐标代入函数y=kx+b中，计算出k、b的值是解题关键.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为提升青少年的身体素质,深圳市在全市中小学推行“阳光体育”活动,某学校为满足学生的需求,准备再购买一些篮球和足球.已知用800元购买篮球的个数比购买足球的个数少2个,足球的单价为篮球单价的
.
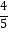（1）求篮球、足球的单价分别为多少元?
（2）如果计划用不多于5200元购买篮球、足球共60个 ,那么至少要购买多少个足球? -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：已知正方形的边长为a，将此正方形按照下面的方法进行剪拼：第一次，先沿正方形的对边中点连线剪开，然后对接为一个长方形，则此长方形的周长为___；第二次，再沿长方形的对边（长方形的宽）中点连线剪开，对接为新的长方形，如此继续下去，第n次得到的长方形的周长为__．
-
科目： 来源： 题型：
查看答案和解析>>【题目】本学期学习了一元一次方程的解法，下面是小亮同学的解题过程：
解方程：
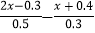＝1解：原方程可化为：
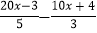＝1…………①方程两边同时乘以15，去分母，得
3（20x﹣3）﹣5（10x+4）＝15…………②
去括号，得60x﹣9﹣50x+20＝15…………③
移项，得60x﹣50x＝15+9﹣20……………④
合并同类项，得10x＝4………………⑤
系数化1，得x＝0.4………………⑥
所以x＝0.4原方程的解
上述小亮的解题过程从第 （填序号）步开始出现错误，
错误的原因是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△OAB中，OA=OB，C为AB中点，以O圆心，OC长为半径作圆，AO与⊙O交于点E，直线OB与⊙O交于点F和D，连接EF、CF，CF与OA交于点G.
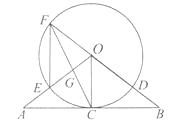
（1）求证：直线AB是⊙O的切线；
（2）求证：OD·EG=OG·EF；
（3）若AB=8，BD=2，求⊙O的半径. -
科目： 来源： 题型：
查看答案和解析>>【题目】填空，完成下列说理过程
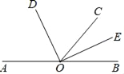
如图，已知点A，O，B在同一条直线上，OE平分∠BOC，∠DOE＝90°
求证：OD是∠AOC的平分线；
证明：如图，因为OE是∠BOC的平分线，
所以∠BOE＝∠COE．（ ）
因为∠DOE＝90°
所以∠DOC+∠ ＝90°
且∠DOA+∠BOE＝180°﹣∠DOE＝ °．
所以∠DOC+∠ ＝∠DOA+∠BOE．
所以∠ ＝∠ ．
所以OD是∠AOC的平分线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx-3经过A（-1,0）、B（3,0）两点，与y轴交于C点，
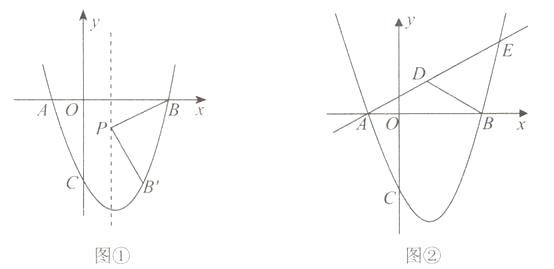
（1）求抛物线的解析式；
（2）如图①，抛物线的对称轴上有一点P，且点P在x轴下方，线段PB绕点P顺时针旋转90°，点B的对应点B′恰好落在抛物线上，求点P的坐标；
（3）如图②，直线y=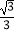
x+ 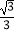交抛物线于A、E两点，点D为线段AE上一点，连接BD，有一动点Q从B点出发，沿线段BD以每秒1个单位的速度运动到D，再沿DE以每秒钟2个单位的速度运动到E，问：是否存在点D，使点Q从点B到E的运动时间最少，若存在，请求出点D的坐标；若不存在，请说明理由.
相关试题
