【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

参考答案:
【答案】(1)110°.(2)∠APC=∠α+∠β,(3)当P在BD延长线上时,∠CPA=∠α﹣∠β;当P在DB延长线上时,∠CPA=∠β﹣∠α.
【解析】
试题(1)过点P作PE∥AB,则有PE∥AB∥CD,根据两直线平行,同旁内角互补得到∠A+∠APE=180°,∠C+∠CPE=180°,再根据∠APC=∠APE+∠CPE和已知∠APE和∠CPE度数即可求出∠APC的角度。(2)过P作PE∥AB交AC于E,则有AB∥PE∥CD,进而得到∠α=∠APE,∠β=∠CPE,再根据∠APC=∠APE+∠CPE,即可用α、β来表示∠APC的度数;(3)根据题意画出图形,当P在BD延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α,当如图所示,当P在DB延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α;
试题解析:
(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
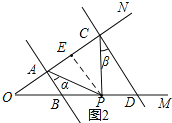
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
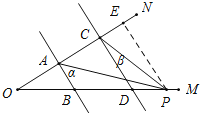
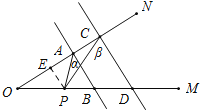
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册)
1≤a<5
5≤a<10
彩色 (单位:元/张)
2.2
2.0
黑白(单位:元/张)
0.7
0.6
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
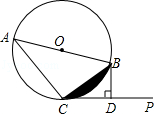
(1)求证:CB2=ABDB;
(2)若⊙O的半径为2,∠BCP=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在甲公司打工.几个月后同时又在乙公司打工.甲公司每月付给他薪金470元,乙公司每月付给他薪金350元.年终小明从这两家公司共获得薪金7620元.问他在甲、乙两公司分别打工几个月?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了进一步了解义务教育阶段学生的体质健康状况,某县从全县九年级学生中随机抽取了部分学生进行了体质抽测.体质抽测的结果分为四个等级:A级:优秀;B级:良好;C级:合格;D级:不合格.并根据抽测结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
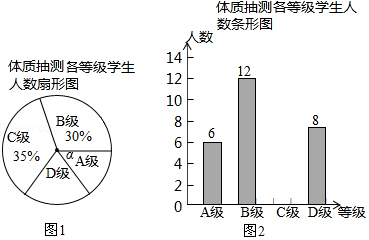
(1)本次抽测的学生人数是人;
(2)图(1)中∠α的度数是 , 并把图(2)条形统计图补充完整;
(3)该县九年级有学生4800名,如果全部参加这次体质测试,请估计不合格的人数为 .
(4)测试老师想从4位同学(分别记为E、F、G、H,其中H为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探索
知识累计
解方程组
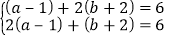
解:设a﹣1=x,b+2=y,原方程组可变为

解方程组得:
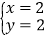 即
即 所以
所以 此种解方程组的方法叫换元法.
此种解方程组的方法叫换元法.(1)拓展提高
运用上述方法解下列方程组:

(2)能力运用
已知关于x,y的方程组
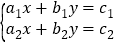 的解为
的解为 ,直接写出关于m、n的方程组
,直接写出关于m、n的方程组 的解为_____________.
的解为_____________.
相关试题

