搜索
【题目】阅读探索
知识累计
解方程组
解：设a﹣1=x，b+2=y，原方程组可变为
解方程组得：
即
所以
此种解方程组的方法叫换元法．
（1）拓展提高
运用上述方法解下列方程组：
（2）能力运用
已知关于x，y的方程组
的解为
，直接写出关于m、n的方程组
的解为_____________．
参考答案：
【答案】（1）
（2）
【解析】
（1）利用换元法把
，
分别看成一个整体把原方程组进行变形求出，继而在求出a和b
（2）利用换元法把5（m+3）,3（n-2）分别看成一个整体把原方程组变形，可得一个新的含有m、n的二元一次方程组，然后求解即可得所求
解： （1）拓展提高
设
1=x，
+2=y，
方程组变形得：
，
解得：
，即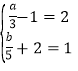
，
解得：
；
（2）能力运用
设
，
可得
，
解得：
，
故答案为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．
(1)按小明的思路，易求得∠APC的度数为_____度；
(2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
(3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在甲公司打工．几个月后同时又在乙公司打工．甲公司每月付给他薪金470元，乙公司每月付给他薪金350元．年终小明从这两家公司共获得薪金7620元．问他在甲、乙两公司分别打工几个月?
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了进一步了解义务教育阶段学生的体质健康状况，某县从全县九年级学生中随机抽取了部分学生进行了体质抽测．体质抽测的结果分为四个等级：A级：优秀；B级：良好；C级：合格；D级：不合格．并根据抽测结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：
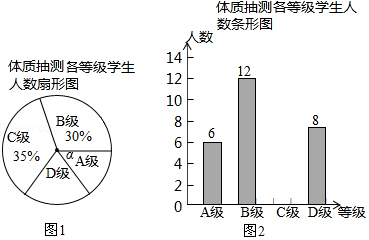
（1）本次抽测的学生人数是人；
（2）图（1）中∠α的度数是 ， 并把图（2）条形统计图补充完整；
（3）该县九年级有学生4800名，如果全部参加这次体质测试，请估计不合格的人数为 ．
（4）测试老师想从4位同学（分别记为E、F、G、H，其中H为小明）中随机选择两位同学了解平时训练情况，请用列表或画树形图的方法求出选中小明的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】小明到某服装专卖店去做社会调查，了解到该专卖店为了微励营业员的工作积极性，实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资，并获得如下信息；
营业员
小张
小王
月销售件数
200
150
月总收入/元
1400
1250
销售每件奖励a元，晋业员月基本工资为b元.
（1）列方程组求a，b的值.
（2）假设月销售件数为x，月总收入为y元，请写出y与x的函数关系式，并求出营业员小张上个月总收入是1700元时，小张上个月卖了多少件服装?
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们知道，一元二次方程x2=﹣1没有实数根，即不存在一个实数的平方等于﹣1．若我们规定一个新数“i”，使其满足i2=﹣1（即方程x2=﹣1有一个根为i）．并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有i1＝i，i2＝﹣1，i3＝i2i＝﹣i，i4＝（i2）2＝（﹣1）2=1，从而对于任意正整数n，我们可以得到i4n+1＝i4ni＝i，同理可得i4n+2＝﹣1，i4n+3＝﹣i，i4n＝1．
计算：（1）i．i2．i3．i4
（2）i+i2+i3+i4+…+i2017+i2018． -
科目： 来源： 题型：
查看答案和解析>>【题目】解方程组:
（1）
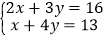(代入法)（2）
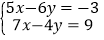(加减法)（3）
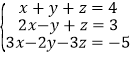
相关试题
