搜索
【题目】计算：
（1）﹣0.5﹣（﹣3 
）+2.75﹣（+7
）
（2）（
+
﹣）×（﹣12）
（3）（﹣2）3÷
×
2
（4）﹣12﹣ 
×[2﹣（﹣4）2]
参考答案：
【答案】（1）﹣2；（2）﹣5；（3）﹣8；（4）-
【解析】
（1）根据有理数的加减法可以解答本题；
（2）根据乘法分配律可以解答本题；
（3）根据有理数的乘除法可以解答本题；
（4）根据有理数的乘法和减法可以解答本题．
（1）﹣0.5﹣（﹣3
）+2.75﹣（+7
）
=（﹣0.5）+3 +2.75+（﹣7.5），
=﹣2；
（2）（
+
﹣）×（﹣12）
=（﹣9）+（﹣2）+6，
=﹣5；
（3）（﹣2）3÷
×
2
=（﹣8）×
，
=﹣8；
（4）﹣12﹣
×[2﹣（﹣4）2]
=﹣1﹣×[2﹣16]
=﹣1﹣×（﹣14）
=﹣1+
=-．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC的周长是20，三边分别为a，b，c.
(1)若b是最大边，求b的取值范围；
(2)若△ABC是三边均不相等的三角形，b是最大边，c是最小边，且b＝3c，a，b，c均为整数，求△ABC的三边长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】图（1）为一波浪式相框（厚度忽略不计），内部可插入占满整个相框的照片一张，如图（2），主视图（不含图中虚线部分）为两端首尾相连的等弧构成，左视图和俯视图均为长方形（单位：cm）：
（1）图中虚线部分的长为cm，俯视图中长方形的长为cm；
（2）求主视图中的弧所在圆的半径；
（3）试计算该相框可插入的照片的最大面积（参考数据：sin22.5°≈
，cos22.5°≈ 
，tan22.5°≈ 
，计算结果保留π）． -
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读下列解题过程，然后回答问题：
解方程：
解：①当
≥0时，原方程可化为： 
，解得
；②当
＜0时，原方程可化为： 
，解得
；所以原方程的解是
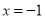或
（1）解方程：
（2）探究：当
为何值时，方程
①无解；②只有一个解；③有两个解。 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，学校有一个长方形广场，在广场的中央设计一个圆形花坛，四角都设计四分之一圆形的花坛．若长方形的长为am，宽为bm，中央圆形的半径和四个四分之一圆形的半径都为rm．
（1）列式表示广场空地的面积；（不写过程，直接写出答案）
（2）学校准备在广场四周种树，七年级四个班的学生在植树节当天进行义务植树，一班植树 x棵，二班植树的棵数比一班的多10棵，三班植树的棵数比二班的2倍少30棵，四班植树的棵数比三班的一半多20棵，求四个班一共植树多少棵？（用含x的式子表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线C1：y1=tx2﹣1（t＞0）和抛物线C2：y2=﹣4（x﹣h）2+1（h≥1）．
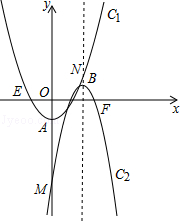
（1）两抛物线的顶点A、B的坐标分别为和；
（2）设抛物线C2的对称轴与抛物线C1交于点N，则t为何值时，A、B、M、N为顶点的四边形是平行四边形．
（3）设抛物线C1与x轴的左交点为点E，抛物线C2与x轴的右边交点为点F，试问，在第（2）问的前提下，四边形AEBF能否为矩形？若能，求出h值；若不能，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，△ACB和△DCE均为等边三角形，若B，D，E在同一直线上，连接AE．
（1）请你在图中找出一个与△AEC全等的三角形：；
（2）∠AEB的度数为；CE，AE，BE的数量关系为 ．
（3）如图2，△ACB是等腰直角三角形，∠AEB=90°，连接CE，过点C作CD⊥CE，交BE于点D，试探究CE，AE，BE的数量关系，并说明理由．
（4）如图3，在正方形ABCD中，CD=5
，点P为正方形ABCD外一点，∠APC=90°，且AP=6，试求点P到CD的距离．
相关试题
