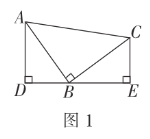
【题目】(1)如图1,在![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() .
.
(2)如图2,已知点![]() ,点
,点![]() ,
,![]() ,
,![]() ,且点
,且点![]() 在第一象限,求
在第一象限,求![]() 所在直线的表达式.
所在直线的表达式.
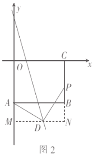
(3)如图3,在长方形![]() 中,
中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别在坐标轴上,点
分别在坐标轴上,点![]() 是线段
是线段![]() 上的动点,点
上的动点,点![]() 是直线
是直线![]() 上的动点且在
上的动点且在![]() 轴的右侧.若
轴的右侧.若![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点![]() 的坐标.
的坐标.


参考答案:
【答案】(1)详见解析;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)通过∠BCE+∠EBC=90°,∠ABD+∠EBC=90°得∠ABD=∠BCE,再结合∠ADC=∠BEC=90°,CB=CA即可得证;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,由(1)可知
,由(1)可知![]() ,
,![]() ,则
,则![]() ,进而求得点C坐标,再结合点A坐标利用待定系数法求解即可;
,进而求得点C坐标,再结合点A坐标利用待定系数法求解即可;
(3)设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,交
,交![]() 延长线于点
延长线于点![]() ,由(1)得
,由(1)得![]() ,进而通过
,进而通过![]() 列出方程求解即可.
列出方程求解即可.
(1)证明:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
(2)解:如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
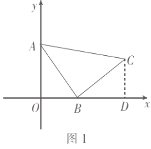
由(1)可知![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设![]() 所在直线的表达式为
所在直线的表达式为![]() ,
,
将![]() ,
,![]() 代入得
代入得![]() 解得
解得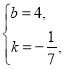
![]() 直线
直线![]() 在直线的表达式为
在直线的表达式为![]() .
.
(3)解:∵点D在y=﹣3x+6上,
∴设点![]() 的坐标为
的坐标为![]() .
.
如图2,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
由题意可得![]() ,(AAS)
,(AAS)
![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数
 是
是 关于
关于 的反比例函数。
的反比例函数。(1)求
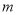 的值;
的值;(2)函数图象在哪些象限?在每个象限内,
 随
随 的增大而怎样变化?
的增大而怎样变化?(3)当
 时,求
时,求 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产
 两种设备,已知每台
两种设备,已知每台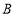 种设备的成本是
种设备的成本是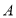 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产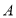 种设备,投人15万元生产
种设备,投人15万元生产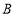 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:(1)
 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?(2)若
 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中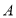 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个装有进水管和出水管的容器,根据实际需要,从某时刻开始的2分钟内只进水不出水,在随后的4分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图所示.
(1)当2≤x≤6时,求y与x的表达式;
(2)请将图象补充完整;
(3)从进水管开始进水起,求该容器内的水量不少于7.5升所持续时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD四条边上的中点分别为E.F.G.H,顺次连接EF.FG.GH.HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH的形状是 ,证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)结合问题(2),请做出图形并且证明
相关试题

