【题目】若函数![]() 是
是![]() 关于
关于![]() 的反比例函数。
的反比例函数。
(1)求![]() 的值;
的值;
(2)函数图象在哪些象限?在每个象限内,![]() 随
随![]() 的增大而怎样变化?
的增大而怎样变化?
(3)当![]() 时,求
时,求![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() ;(2)第二象限、第四象限;在每个象限内,
;(2)第二象限、第四象限;在每个象限内,![]() 随
随![]() 的增大而增大;(3)
的增大而增大;(3)![]()
【解析】
(1)根据反比例函数的定义列出关于m的不等式和方程,求出m的值即可;
(2)根据反比例函数的性质即可得出结论;
(3)分别令x=-3,x=-![]() ,求出y的对应值即可.
,求出y的对应值即可.
(1)∵函数![]() 是y关于x的反比例函数,
是y关于x的反比例函数,
∴![]() ,
,
解得m=-2;
(2)∵m=-2,
∴反比例函数的关系式为:y=-![]() .
.
∵-4<0,
∴函数图象的两个分支分别位于第二、四象限,且在每个象限内,y随x的增大而增大;
(3)∵反比例函数的关系式为:y=-![]() ,
,
∴当x=-3时,y=![]() ;
;
当x=-![]() 时,y=8,
时,y=8,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )

A. 7 B. 8 C. 12 D. 14
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎解方程
 时出现了错误,其解答过程如下:
时出现了错误,其解答过程如下:解:方程两边都乘以
 ,得
,得 ,(第1步)
,(第1步)移项,合并同类项,得
 ,(第2步)
,(第2步)经检验,
 是原方程的解.(第3步)
是原方程的解.(第3步)(1)小马虎解答过程是从第______步开始出错的,出错的原因是___________;
(2)请写出此题正确的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一幅三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.

(1)求证:CF∥AB.
(2)求∠DFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )

A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产
 两种设备,已知每台
两种设备,已知每台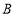 种设备的成本是
种设备的成本是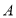 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产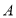 种设备,投人15万元生产
种设备,投人15万元生产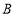 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:(1)
 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?(2)若
 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中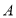 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在
 中,
中, ,
, ,直线
,直线 经过点
经过点 ,过点
,过点 作
作 于点
于点 ,过点
,过点 作
作 于点
于点 ,求证:
,求证: .
.(2)如图2,已知点
 ,点
,点 ,
, ,
, ,且点
,且点 在第一象限,求
在第一象限,求 所在直线的表达式.
所在直线的表达式.(3)如图3,在长方形
 中,
中, 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点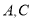 分别在坐标轴上,点
分别在坐标轴上,点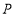 是线段
是线段 上的动点,点
上的动点,点 是直线
是直线 上的动点且在
上的动点且在 轴的右侧.若
轴的右侧.若 是以点
是以点 为直角顶点的等腰直角三角形,请求出点
为直角顶点的等腰直角三角形,请求出点 的坐标.
的坐标.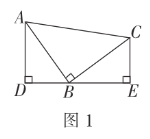


相关试题

