【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上. 
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(2)如图2,AC:AB=1: ![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.
参考答案:
【答案】
(1)证明:如图1,
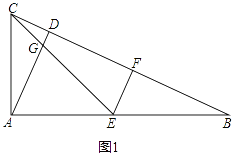
在△ABC中,∵∠CAB=90°,AD⊥BC于点D,
∴∠CAD=∠B=90°﹣∠ACB.
∵AC:AB=1:2,
∴AB=2AC,
∵点E为AB的中点,
∴AB=2BE,
∴AC=BE.
在△ACD与△BEF中,
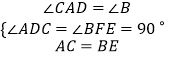 ,
,
∴△ACD≌△BEF,
∴CD=EF,即EF=CD
(2)解:如图2,作EH⊥AD于H,EQ⊥BC于Q,
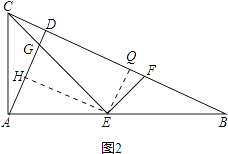
∵EH⊥AD,EQ⊥BC,AD⊥BC,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°﹣∠QEG,
又∵∠EQF=∠EHG=90°,
∴△EFQ∽△EGH,
∴EF:EG=EQ:EH.
∵AC:AB=1: ![]() ,∠CAB=90°,
,∠CAB=90°,
∴∠B=30°.
在△BEQ中,∵∠BQE=90°,
∴sinB= ![]() =
= ![]() ,
,
∴EQ= ![]() BE.
BE.
在△AEH中,∵∠AHE=90°,∠AEH=∠B=30°,
∴cos∠AEH= ![]() =
= ![]() ,
,
∴EH= ![]() AE.
AE.
∵点E为AB的中点,
∴BE=AE,
∴EF:EG=EQ:EH= ![]() BE:
BE: ![]() AE=1:
AE=1: ![]() =
= ![]() :3.
:3.
【解析】(1)根据同角的余角相等得出∠CAD=∠B,根据AC:AB=1:2及点E为AB的中点,得出AC=BE,再利用AAS证明△ACD≌△BEF,即可得出EF=CD;(2)作EH⊥AD于H,EQ⊥BC于Q,先证明四边形EQDH是矩形,得出∠QEH=90°,则∠FEQ=∠GEH,再由两角对应相等的两三角形相似证明△EFQ∽△EGH,得出EF:EG=EQ:EH,然后在△BEQ中,根据正弦函数的定义得出EQ= ![]() BE,在△AEH中,根据余弦函数的定义得出EH=
BE,在△AEH中,根据余弦函数的定义得出EH= ![]() AE,又BE=AE,进而求出EF:EG的值.
AE,又BE=AE,进而求出EF:EG的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一张圆心角为45°的扇形纸板剪得一个边长为1的正方形,则扇形纸板的面积是cm2(结果保留π)

-
科目: 来源: 题型:
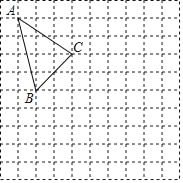
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,4)C(0,2)
(1)请在网格所在的平面内建立平面直角坐标系,并写出点B的坐标;
(2)画出△ABC关于原点对称的图形△A1B1C1;
(3)求△ABC的面积;
(4)在x轴上存在一点P,使PA+PB的值最小,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图1,矩形ABCD中,BC=2AB,则称ABCD为方形.
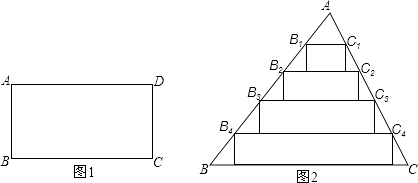
(1)设a,b是方形的一组邻边长,写出a,b的值(一组即可).
(2)在△ABC中,将AB,AC分别五等分,连结两边对应的等分点,以这些连结线为一边作矩形,使这些矩形的边B1C1 , B2C2 , B3C3 , B4C4的对边分别在B2C2 , B3C3 , B4C4 , BC上,如图2所示.
①若BC=25,BC边上的高为20,判断以B1C1为一边的矩形是不是方形?为什么?
②若以B3C3为一边的矩形为方形,求BC与BC边上的高之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.

(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分)
八年1班
80 86 88 80 88 99 80 74 91 89
八年2班
85 85 87 97 85 76 88 77 87 88
八年3班
82 80 78 78 81 96 97 87 92 84
解答下列问题:
(1)请填写下表:
平均数(分)
众数(分)
中位数(分)
八年1班
85.5
87
八年2班
85.5
85
八年3班
78
83
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF= .
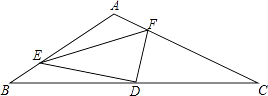
相关试题

