搜索
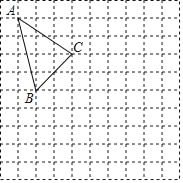
【题目】如图，在正方形网格中，每个小正方形的边长为1，格点△ABC（顶点在网格线的交点上）的顶点A、C的坐标分别为A（﹣3，4）C（0，2）
（1）请在网格所在的平面内建立平面直角坐标系，并写出点B的坐标；
（2）画出△ABC关于原点对称的图形△A1B1C1；
（3）求△ABC的面积；
（4）在x轴上存在一点P，使PA+PB的值最小，请直接写出点P的坐标．
参考答案：
【答案】（1）坐标系详见解析，点B的坐标（﹣2，0）；（2）详见解析；（3）5；（4）点P的坐标（﹣2，0）．
【解析】
（1）根据A、C点坐标，作出的平面直角坐标系即可，根据作出的平面直角坐标系写出B点的坐标即可；
（2）根据原点对称的特点画出图形即可；
（3）利用矩形面积减去周围三角形面积得出即可；
（4）根据轴对称的性质解答即可．
解：（1）如图所示：
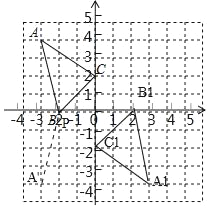
点B的坐标（-2，0）；
（2）如图所示，△A1B1C1即为所求；
（3）△ABC的面积
=5；
（4）点P的坐标（-2，0）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校体育组为了了解学生喜欢的体育项目，从全校同学中随机抽取了若干名同学进行调查，每位同学从乒乓球、篮球、羽毛球、排球、跳绳中选择一项最喜欢的项目，并将调查的结果绘制成如下的两幅统计图．根据以上统计图，解答下列问题：
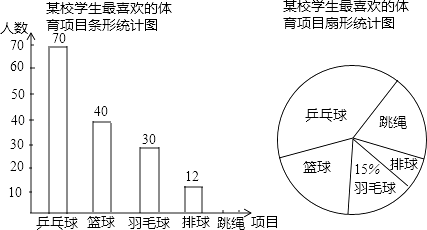
（1）这次被调查的共有多少名同学？并补全条形统计图．
（2）若全校有1200名同学，估计全校最喜欢篮球和排球的共有多少名同学？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，伞不论张开还是收紧，伞柄AP始终平分同一平面内两条伞架所成的角∠BAC，当伞收紧时，结点D与点M重合，且点A、E、D在同一条直线上，已知部分伞架的长度如下：单位：cm
伞架
DE
DF
AE
AF
AB
AC
长度
36
36
36
36
86
86
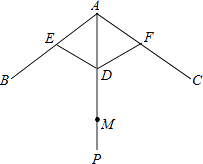
（1）求AM的长．
（2）当∠BAC=104°时，求AD的长（精确到1cm）． 备用数据：sin52°=0.788，cos52°=0.6157，tan52°=1.2799． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一张圆心角为45°的扇形纸板剪得一个边长为1的正方形，则扇形纸板的面积是cm2（结果保留π）
-
科目： 来源： 题型：
查看答案和解析>>【题目】若一个矩形的一边是另一边的两倍，则称这个矩形为方形，如图1，矩形ABCD中，BC=2AB，则称ABCD为方形．
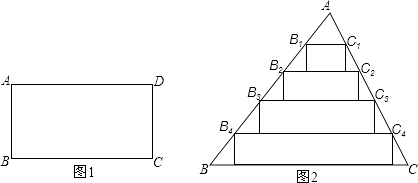
（1）设a，b是方形的一组邻边长，写出a，b的值（一组即可）．
（2）在△ABC中，将AB，AC分别五等分，连结两边对应的等分点，以这些连结线为一边作矩形，使这些矩形的边B1C1 ， B2C2 ， B3C3 ， B4C4的对边分别在B2C2 ， B3C3 ， B4C4 ， BC上，如图2所示．
①若BC=25，BC边上的高为20，判断以B1C1为一边的矩形是不是方形？为什么？
②若以B3C3为一边的矩形为方形，求BC与BC边上的高之比． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G，点F在BC上．
（1）如图1，AC：AB=1：2，EF⊥CB，求证：EF=CD．
（2）如图2，AC：AB=1：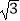
，EF⊥CE，求EF：EG的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=（x﹣3）（x+1）与x轴交于A，B两点（点A在点B左侧），与y轴交于点C，点D为顶点．
（1）求点B及点D的坐标．
（2）连结BD，CD，抛物线的对称轴与x轴交于点E．
①若线段BD上一点P，使∠DCP=∠BDE，求点P的坐标．
②若抛物线上一点M，作MN⊥CD，交直线CD于点N，使∠CMN=∠BDE，求点M的坐标．
相关试题
