【题目】已知抛物线y=﹣x2+2x+3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
参考答案:
【答案】解:(1)令y=0,则﹣x2+2x+3=0,
解得:x1=﹣1,x2=3.
则A的坐标是(﹣1,0),B的坐标是(3,0).
y=﹣x2+2x+3=﹣(x﹣1)2+4,
则对称轴是x=1,顶点C的坐标是(1,4);
(2)D的坐标是(1,﹣4).
AB=3﹣(﹣1)=4,CD=4﹣(﹣4)=8,
则四边形ACBD的面积是:![]() ABCD=
ABCD=![]() ×4×8=16.
×4×8=16.
【解析】(1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;
(2)首先求得D的坐标,然后利用面积公式即可求解.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是多项式2m2n-m3n2-m-2的次数,c是单项式-2xy2的系数,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;

(2)若动点P,Q同时从A,B出发沿数轴负方向运动,点P的速度是每秒
 个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?
个单位长度,点Q的速度是每秒2个单位长度,求运动几秒后,点Q可以追上点P?(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于10,请直接写出所有点M对应的数.(不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从-1,1,2这三个数字中,随机抽取一个数记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为
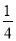 ,且使关于x的不等式组
,且使关于x的不等式组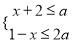 有解的概率为________.
有解的概率为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, △ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连结EC
⑴求∠ECD的度数;
⑵若CE=5,求CB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;
(2)若AB=12,AD=8,CD=15,求DB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,且AB=4
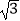 . 点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
. 点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为2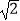 , 直接写出∠BAF的度数.
, 直接写出∠BAF的度数.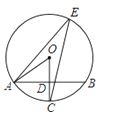
相关试题

