Question

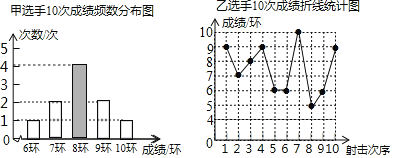
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图（部分）如图所示：

根据以上信息，请解答下面的问题；

选手	A平均数	中位数	众数	方差
甲	a	8	8	c
乙	7.5	b	6和9	2.65

（1）补全甲选手10次成绩频数分布图．

（2）a＝　 　，b＝　 　，c＝　 　．

（3）教练根据两名选手手的10次成绩，决定选甲选手参加射击比赛，教练的理由是什么？（至少从两个不同角度说明理由）．

Answer 1

【答案】（1）4；（2）8、1.2、7.5；（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的方差小，说明甲的成绩稳定．

【解析】

（1）根据甲的成绩频数分布图及题意列出10﹣（1+2+2+1），计算即可得到答案；

（2）根据平均数公式、中位数的求法和方差公式计算得到答案；

（3）从平均数和方差进行分析即可得到答案.

解：（1）甲选手命中8环的次数为10﹣（1+2+2+1）＝4，

补全图形如下：

（2）a＝＝8（环），

c＝×[（6﹣8）2+2×（7﹣8）2+4×（8﹣8）2+2×（9﹣8）2+（10﹣8）2]＝1.2，

b＝＝7.5，

故答案为：8、1.2、7.5；

（3）从平均数看，甲成绩优于乙的成绩；从方差看，甲的方差小，说明甲的成绩稳定．