【题目】如图,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,则该运动员此次掷铅球的成绩是( )
,则该运动员此次掷铅球的成绩是( )
A.6m
B.12m
C.8m
D.10m
参考答案:
【答案】D
【解析】解:把y=0代入y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() 得:
得:
﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =0,
=0,
解之得:x1=10,x2=﹣2.
又x>0,解得x=10.
所以答案是:D.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 为
为 的高,
的高,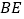 是
是 的角平分线,若
的角平分线,若 ,
,
(1)求
 的度数;
的度数;(2)若点F为线段
 上任一点,当
上任一点,当 为直角三角形时,求
为直角三角形时,求 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:
(1)如图,我们将图(1)所示的凹四边形称为“镖形”.在“镖形”图中,
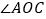 与
与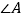 、
、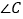 、
、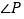 的数量关系为____.
的数量关系为____.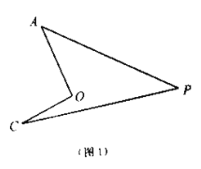
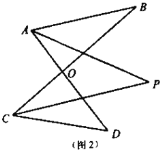
(2)如图(2),已知
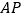 平分
平分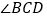 ,
,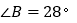 ,
,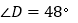 ,求
,求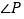 的度数.
的度数.由(1)结论得:
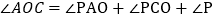
所以
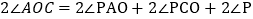 即
即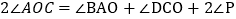
因为
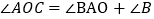
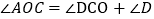
所以
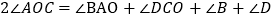
所以
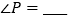 .
.解决问题:
(1)如图(3),直线
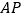 平分
平分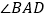 ,
, 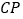 平分
平分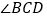 的外角
的外角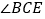 ,猜想
,猜想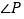 与
与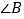 、
、 的数量关系是______;
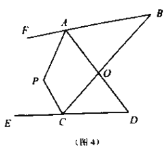
的数量关系是______;(2)如图(4),直线
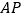 平分
平分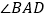 的外角
的外角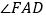 ,
, 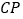 平分
平分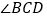 的外角
的外角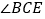 ,猜想
,猜想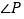 与
与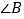 、
、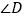 的数量关系,并说明理由.
的数量关系,并说明理由.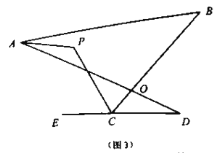
-
科目: 来源: 题型:
查看答案和解析>>【题目】足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t=
 ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某山区有23名中、小学生因贫困失学需要捐助,资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,我校初中学生每个年级各自分别捐助的贫困中学生和小学生的人数情况如下表:

(1)求a,b的值.
(2)九年级学生的捐款解决了其余贫困中小学生的学习费用,求九年级学生可捐助的贫困生中、小学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,排球运动员站在点O处练习发球,将球从D点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )

A.球不会过网
B.球会过球网但不会出界
C.球会过球网并会出界
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手
A平均数
中位数
众数
方差
甲
a
8
8
c
乙
7.5
b
6和9
2.65
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
相关试题

