【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,C(0,a),D(b,a),其中a,b满足关系式:|a+3|+(b-a+1)2=0.
(1)a=___,b=___,△BCD的面积为______;
(2)如图2,若AC⊥BC,点P线段OC上一点,连接BP,延长BP交AC于点Q,当∠CPQ=∠CQP时,求证:BP平分∠ABC;
(3)如图3,若AC⊥BC,点E是点A与点B之间一动点,连接CE,CB始终平分∠ECF,当点E在点A与点B之间运动时,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.



参考答案:
【答案】 -3 -4 6
【解析】分析:(1)求出CD的长度,再根据三角形的面积公式列式计算即可得解;
(2)根据等角的余角相等解答即可;
(3)首先证明∠ACD=∠ACE,推出∠DCE=2∠ACD,再证明∠ACD=∠BCO,∠BEC=∠DCE=2∠ACD即可解决问题;
详解:(1)解:如图1中,
∵|a+3|+(b-a+1)2=0,
∴a=-3,b=4,
∵点C(0,-3),D(-4,-3),
∴CD=4,且CD∥x轴,
∴△BCD的面积=1212×4×3=6;
故答案为-3,-4,6.
(2)证明:如图2中,
∵∠CPQ=∠CQP=∠OPB,AC⊥BC,
∴∠CBQ+∠CQP=90°,
又∵∠ABQ+∠CPQ=90°,
∴∠ABQ=∠CBQ,
∴BQ平分∠CBA.
(3)解:如图3中,结论:![]() =定值=2.
=定值=2.
理由:∵AC⊥BC,
∴∠ACB=90°,
∴∠ACD+∠BCF=90°,
∵CB平分∠ECF,
∴∠ECB=∠BCF,
∴∠ACD+∠ECB=90°,
∵∠ACE+∠ECB=90°,
∴∠ACD=∠ACE,
∴∠DCE=2∠ACD,
∵∠ACD+∠ACO=90°,∠BCO+∠ACO=90°,
∴∠ACD=∠BCO,
∵C(0,-3),D(-4,-3),
∴CD∥AB,
∠BEC=∠DCE=2∠ACD,
∴∠BEC=2∠BCO,
∴![]() =2.
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小高从家骑自行车去学校上学,先走上坡路到达点A,再走下坡路到达点B,最后走平路到达学校,所用的时间与路程的关系如图所示.放学后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上学时一致,那么他从学校到家需要的时间是( )
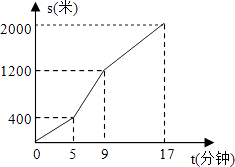
A.14分钟
B.17分钟
C.18分钟
D.20分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=4,CE=
 ,则△ABC的面积为( )
,则△ABC的面积为( ) 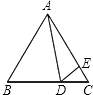
A.8
B.15
C.9
D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个)
售价(元/个)
电饭煲
200
250
电压锅
160
200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)7﹣3(x﹣1)=2(4﹣x)
(2)|2x+1|=5
(3)

(4)
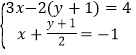
(5)
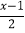 ≤1﹣
≤1﹣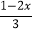
(6)
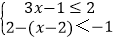 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
某中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地校参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量
租金(元)
A
x
45x
400x
B
5﹣x
(2)若要保证租车费用不超过1900元,求x的最大值.
-
科目: 来源: 题型:
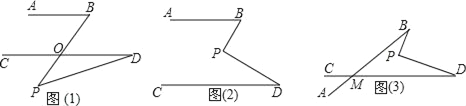
查看答案和解析>>【题目】(1)如图(1),AB∥CD,点P在AB,CD外部,若∠B=50°,∠D=25°,则∠BPD= °
(2)如图(2),AB∥CD,点P在AB,CD内部,则∠B,∠D,∠BPD之间有何数量关系?证明你的结论.
(3)在图(2)中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M,如图(3),若∠BPD=90°,∠BMD=40°,求∠B+∠D的度数.
相关试题

