【题目】小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A、B、D三点在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8. 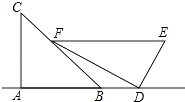
(1)试求点F到AD的距离.
(2)试求BD的长.
参考答案:
【答案】
(1)解:如图,过点F作FM⊥AD于点M,
在△EDF中,∠EDF=90°,∠E=60°,DE=8,
则∠DFE=30°,
故EF=2DE=16,
DF= ![]() =
= ![]() =8
=8 ![]() ,
,
∵AB∥EF,
∴∠FDM=∠DFE=30°,
在Rt△FMD中,MF= ![]() DF=8
DF=8 ![]() ×
× ![]() =4
=4 ![]() ,
,
即点F与AD之间的距离为:4 ![]()
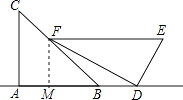
(2)解:在Rt△FMD中,DM= ![]() =
= ![]() =12,
=12,
∵∠C=45°,∠CAB=90°,
∴∠CBA=45°,
又∵∠FMB=90°,
△FMB是等腰直角三角形,
∴MB=FM=4 ![]() ,
,
∴BD=MD﹣FM=12﹣4 ![]()
【解析】(1)根据题意得出∠DFE=30°,则EF=2DE=16,进而利用勾股定理得出DF的长,进而得出答案;(2)直接利用勾股定理得出DM的长,进而得出MB=FM,求出答案.
【考点精析】根据题目的已知条件,利用平行线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>b,下列关系式中一定正确的是()
A. ﹣a>﹣b B. 2a<2b C. 2﹣a<2﹣b D. a2>ab
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图:
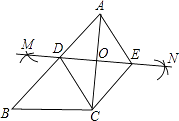
①分别以A、C为圆心,以大于 AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积. -
科目: 来源: 题型:
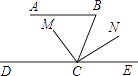
查看答案和解析>>【题目】爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.小明稍加思索,就做出来了,你知道他是怎样解的吗?请把你的推理过程写下来吧.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=
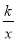 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=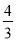 ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x﹣1)=0的解是( )
A.x=0
B.x=1
C.x1=0,x2=﹣1
D.x1=0,x2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=
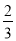 ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.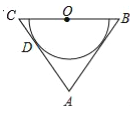
相关试题

