【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
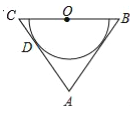
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据锐角三角函数,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
试题解析:(1)证明:如图1,
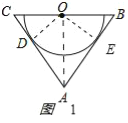
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=![]() ,AB=12,得OB=8.
,AB=12,得OB=8.
由勾股定理,得AO=4![]() .
.
由三角形的面积,得S△AOB=![]() ABOE=
ABOE=![]() OBAO,
OBAO,
∴OE=![]() =
=![]() ,
,
即半圆O所在圆的半径是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板按如图所示的位置摆放,A、B、D三点在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8.
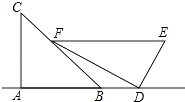
(1)试求点F到AD的距离.
(2)试求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=
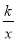 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=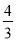 ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x(x﹣1)=0的解是( )
A.x=0
B.x=1
C.x1=0,x2=﹣1
D.x1=0,x2=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在∠AOB内有一点P.
(1)过P画l1∥OA;过P画l2∥OB;
(2)猜想l1与l2相交的角与∠O的大小有怎样关系?(可以用量角器量一下)
(3)你能用你所学的知识证明(3)的结论吗?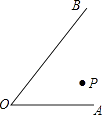
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
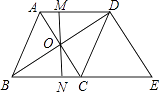
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3+a3=26a
B.3a﹣2a=a
C.3a2b﹣4b2a=﹣a2b
D.(﹣a)2=﹣a2
相关试题

