【题目】如图:数轴上有A、B两点,分别对应的数为a,b,已知(a+1)2与|b﹣3|互为相反数.点P为数轴上一动点,对应为x.
(1)a= ;b=
(2)若点P到点A和点B的距离相等,则点P对应的数是
(3)数轴上是否存在点P,使点P到点A和点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,问几分钟时点P到点A、点B的距离相等?
参考答案:
【答案】(1) ﹣1,3;(2)1;(3) x1=﹣1.5,x2=3.5;(4)4;(5) ![]() 分钟时点P到点A、点B的距离相等
分钟时点P到点A、点B的距离相等
【解析】
(1)根据(a+1)2与|b-3|互为相反数,可以求得a、b的值;
(2)根据题意可以得到关于x的方程,从而可以求得x的值;
(3)根据题意可以列出关于x的方程,本题得以解决;
(4)根据题意,利用分类讨论的思想可以解答本题;
(5)根据题意可以列出相应的方程,本题得以解决.
解:(1)∵(a+1)2与|b﹣3|互为相反数,
∴a+1=0,b﹣3=0,
解得,a=﹣1,b=3,
故答案为:﹣1,3;
(2)由题意可得,
|x﹣(﹣1)|=|x﹣3|,
解得,x=1,
故答案为:1;
(3)数轴上存在点P,使点P到点A和点B的距离之和为5,
由题意可得,
|x﹣(﹣1)|+|x﹣3|=5,
解得,x1=﹣1.5,x2=3.5;
(4)∵a=﹣1,b=3,
∴|x﹣a|+|x﹣b|=|x﹣(﹣1)|+|x﹣3|=|x+1|+|x﹣3|,
当x>3时,|x+1|+|x﹣3|=x+1+x﹣3=2x﹣2>4,
当﹣1≤x≤3时,|x+1|+|x﹣3|=x+1+3﹣x=4,
当x<﹣1时,|x+1|+|x﹣3|=﹣x﹣1+3﹣x=﹣2x+2>4,
∴|x+1|+|x﹣3|的最小值是4,
故答案为:4;
(5)设t分钟时点P到点A、点B的距离相等,
﹣t﹣(﹣1﹣5t)=t+3,
解得,t=![]() ,
,
答:![]() 分钟时点P到点A、点B的距离相等.
分钟时点P到点A、点B的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点到原点的距离相等.
(1)用“>”“=”“<”填空:b 0,a+b 0,a﹣c 0,b﹣c 0,a+c 0;
(2)化简|a+b|+|a﹣c|﹣|b|+|a|+|c|+|a+c|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=15,AC=20,BC边上高AD=12,则BC的长为( )
A. 25 B. 7 C. 25或7 D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校要成立一支由6名女生组成的礼仪队,初三两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如表:
平均数
标准差
中位数
甲队
1.72
0.038
乙队
0.025
1.70
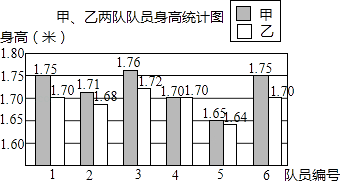
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪一队将被录取?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
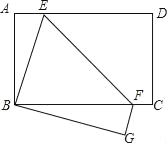
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.

(1)求证:AC是⊙O的切线;
(2)已知sinA= ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
相关试题

