【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA= ![]() ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
参考答案:
【答案】
(1)
解:连接OE.

∵OB=OE
∴∠OBE=∠OEB
∵BE是∠ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是⊙O的切线
(2)
解:连接OF.

∵sinA= ![]() ,∴∠A=30°
,∴∠A=30°
∵⊙O的半径为4,∴AO=2OE=8,
∴AE=4 ![]() ,∠AOE=60°,∴AB=12,
,∠AOE=60°,∴AB=12,
∴BC= ![]() AB=6,AC=6
AB=6,AC=6 ![]() ,
,
∴CE=AC﹣AE=2 ![]() .
.
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,∴∠EOF=60°.
∴S梯形OECF= ![]() (2+4)×2
(2+4)×2 ![]() =6
=6 ![]() .
.
S扇形EOF= ![]() =
= ![]()
∴S阴影部分=S梯形OECF﹣S扇形EOF=6 ![]() ﹣
﹣ ![]()
【解析】(1)连接OE.根据OB=OE得到∠OBE=∠OEB,然后再根据BE是△ABC的角平分线得到∠OEB=∠EBC,从而判定OE∥BC,最后根据∠C=90°得到∠AEO=∠C=90°证得结论AC是⊙O的切线. (2)连接OF,利用S阴影部分=S梯形OECF﹣S扇形EOF求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:数轴上有A、B两点,分别对应的数为a,b,已知(a+1)2与|b﹣3|互为相反数.点P为数轴上一动点,对应为x.

(1)a= ;b=
(2)若点P到点A和点B的距离相等,则点P对应的数是
(3)数轴上是否存在点P,使点P到点A和点B的距离之和为5?若存在,请求出x的值;若不存在,说明理由;
(4)|x﹣a|+|x﹣b|的最小值=
(5)当点P以每分钟1个单位长度的速度从O点向左运动,点A以每分钟5个单位长度向左运动,问几分钟时点P到点A、点B的距离相等?
-
科目: 来源: 题型:
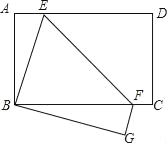
查看答案和解析>>【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>1时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息:
自来水销售价格
污水处理价格
每户每月用水量
单价:元/吨
单价:元/吨
17吨以下
a
0.80
超过17吨但不超过30吨的部分
b
0.80
超过30吨的部分
6.00
0.80
(说明:①每户产生的污水量等于该户自来水用水量;②水费=自来水费用+污水处理费用)
已知小王家2012年4月份用水20吨,交水费66元;5月份用水25吨,交水费91元.
(1)求a、b的值;
(2)随着夏天的到来,用水量将增加.为了节省开支,小王计划把6月份的水费控制在不超过家庭月收入的2%.若小王家的月收入为9200元,则小王家6月份最多能用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
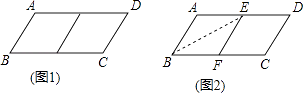
(1)判断与推理:
①邻边长分别为2和3的平行四边形是阶准菱形;
(2)小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE.请证明四边形ABFE是菱形.
(3)操作、探究与计算:
①已知ABCD的邻边长分别为1,a(a>1),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=6b+r,b=5r,请写出ABCD是几阶准菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
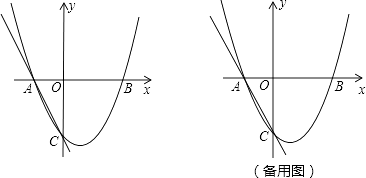
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;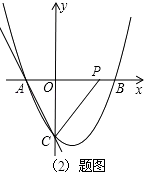
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为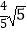 ,求点M的坐标.
,求点M的坐标.
相关试题

