【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:

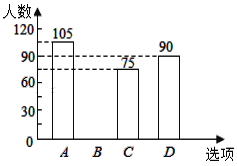
请结合统计图表,回答下列问题:
(1)本次调查的学生共____人,a=______, 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
参考答案:
【答案】(1)300,10%,统计图见详解;(2)700人;(3)![]() .
.
【解析】
(1)根据统计图中![]() 类人数与它所占的百分比可得到调查的总人数,利用百分比之和为1可得
类人数与它所占的百分比可得到调查的总人数,利用百分比之和为1可得![]() 的值,用总人数乘以
的值,用总人数乘以![]() 的百分比得出其人数即可补全条形统计图;
的百分比得出其人数即可补全条形统计图;
(2)总人数乘以样本中![]() 的百分比即可得;
的百分比即可得;
(3)画树状图展示所有12种等可能的结果数,再找出某班抽到的两种形式有一种是“唱歌”的结果数,然后根据概率公式求解.
解:(1)本次调查的总人数为![]() (人
(人![]() ,
,
则![]() ,
,
![]() 选项的人数为
选项的人数为![]() ,
,
补全条形图如下:

故答案为:300,![]() ;
;
(2)![]() (人
(人![]() ,
,
答:估计该校喜欢“唱歌”这种宣传形式的学生约有700人;
(3)画树状图为:

共有12种等可能的结果数,其中抽到的两种形式有一种是“唱歌”的结果数为6,
![]() 某班抽到的两种形式有一种是“唱歌”的概率为
某班抽到的两种形式有一种是“唱歌”的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-
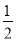 x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=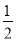 x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )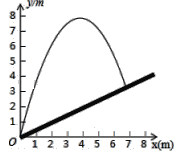
A.斜坡的坡度为1: 2
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知将抛物线
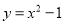 沿
沿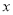 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点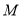 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点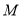 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线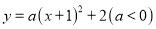 沿
沿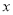 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则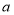 的取值范围是( )
的取值范围是( )
A.
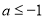 B.
B.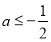 C.
C.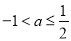 D.
D.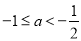
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年8月高邮高铁将通车,高邮至北京的路程约为900km,甲、乙两人从高邮出发,分别乘坐汽车A与高铁B前往北京.已知A车的平均速度比B车的平均速度慢150km/h,A车的行驶时间是B车的行驶时间的2.5倍,两车的行驶时间分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A (1, 0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′ 恰在反比例函数y=
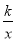 (x>0)的图象上.
(x>0)的图象上.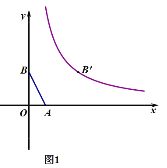
(1)求k的值;
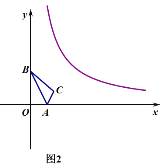
(2)如图2,将△AOB (点O为坐标原点)沿AB翻折得到△ACB,求点C的坐标;
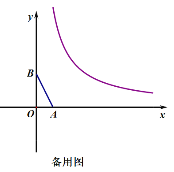
(3)是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF (即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=
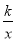 (x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
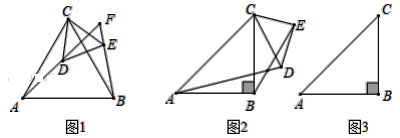
①求证:AD=BE;
②求∠AFB的度数.
(2)如图2,△ABC和△CDE均为等腰直角三角形,∠ABC=∠DEC=90°,直线AD和直线BE交于点F.
①求证:AD=
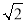 BE;
BE;②若AB=BC=3,DE=EC=
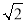 .将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
.将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线y=ax2+bx+c (a≠0)的顶点为M (1,9), 经过抛物线上的两点A(-3,-7)和B (3, m)的直线交抛物线的对称轴于点C.

(1)求抛物线的解析式和直线AB的解析式;
(2)在抛物线上是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)若点P在抛物线上,点Q在x轴上,当以点A、M、P、Q为顶点的四边形是平行四边形时,直接写出满足足条件的点P的坐标.
相关试题

