【题目】如图,已知将抛物线![]() 沿
沿![]() 轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点
轴向上翻折与所得抛物线围成一个封闭区域(包括边界),在这个区域内有5个整点(点![]() 满足横、纵坐标都为整数,则把点
满足横、纵坐标都为整数,则把点![]() 叫做“整点”).现将抛物线
叫做“整点”).现将抛物线![]() 沿
沿![]() 轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则
轴向下翻折,所得抛物线与原抛物线所围成的封闭区域内(包括边界)恰有11个整点,则![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
画出图象,利用图象可得m的取值范围
解:
∵ ![]()
∴该抛物线开口向下,顶点(-1,2),对称轴是直线x=-1.
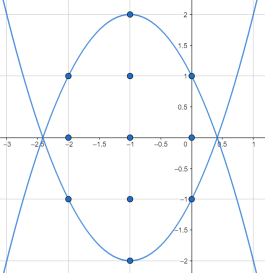
∴点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)符合题意,此时x轴.上的点(-2, 0)、(0, 0)也符合题意,
将(0,1)代入![]() 得到1=a+2.解得a=-1.
得到1=a+2.解得a=-1.
将(1, 0)代入![]() 得到0= 4a+2.解得a=
得到0= 4a+2.解得a=![]()
∵有11个整点,
∴点(0,-1)、点(-2, -1)、点(-2,1)、点(0,1)也必须符合题意.
综上可知:当![]() 时,点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)、点(-2, 0)、(0,0)、点(0,-1)、点(-2,-1)、点(-2,1)、点(0, 1),共有11个整点符合题意,
时,点(-1,2)、点(-1,1)、点(-1, 0)、点(-1,-1)、点(-1,-2)、点(-2, 0)、(0,0)、点(0,-1)、点(-2,-1)、点(-2,1)、点(0, 1),共有11个整点符合题意,
故选: D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.
(1)求证:AC平分∠BAE;
(2)若AC=2CE=6,求⊙O的半径;
(3)请探索:线段AD,BD,CD之间有何数量关系?请证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将含30°角的直角三角板ABC(∠A=30°)绕其直角顶点C顺时针旋转α角(0°<α<90°),得到Rt△A′B′C,A′C与AB交于点D,过点D作DE∥A′B′交CB′于点E,连接BE.易知,在旋转过程中,△BDE为直角三角形.设BC=1,AD=x,△BDE的面积为S.
(1)当α=30°时,求x的值.
(2)求S与x的函数关系式,并写出x的取值范围;
(3)以点E为圆心,BE为半径作⊙E,当S=
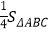 时,判断⊙E与A′C的位置关系,并求相应的tanα值.
时,判断⊙E与A′C的位置关系,并求相应的tanα值.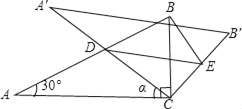
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-
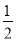 x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=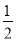 x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )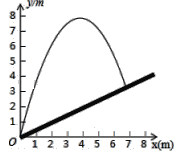
A.斜坡的坡度为1: 2
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年8月高邮高铁将通车,高邮至北京的路程约为900km,甲、乙两人从高邮出发,分别乘坐汽车A与高铁B前往北京.已知A车的平均速度比B车的平均速度慢150km/h,A车的行驶时间是B车的行驶时间的2.5倍,两车的行驶时间分别为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在艺术节宣传活动中,采用了四种宣传形式:A唱歌、B舞蹈、C朗诵、D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:

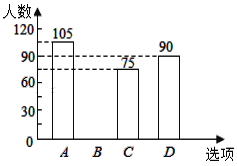
请结合统计图表,回答下列问题:
(1)本次调查的学生共____人,a=______, 并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式有一种是“唱歌”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点A (1, 0),B(0,2),将点B沿x轴正方向平移3个单位长度得到对应点B′,点B′ 恰在反比例函数y=
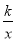 (x>0)的图象上.
(x>0)的图象上.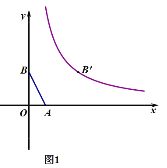
(1)求k的值;
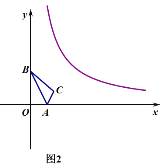
(2)如图2,将△AOB (点O为坐标原点)沿AB翻折得到△ACB,求点C的坐标;
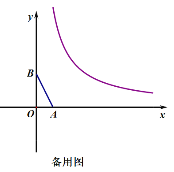
(3)是否存在这样的点P,以P为位似中心,将△AOB放大为原来的两倍后得到△DEF (即△DEF∽△AOB,且相似比为2),使得点D、F恰好在反比例函数y=
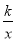 (x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(x>0) 的图象上?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
相关试题

