搜索
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D．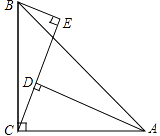 
（1）求证：△ADC≌△CEB．
（2）AD=5cm，DE=3cm，求BE的长度．
参考答案：
【答案】
（1）证明：如图，∵AD⊥CE，∠ACB=90°，
∴∠ADC=∠ACB=90°，
∴∠BCE=∠CAD（同角的余角相等）．
在△ADC与△CEB中，
，
∴△ADC≌△CEB（AAS）
（2）由（1）知，△ADC≌△CEB，则AD=CE=5cm，CD=BE．
如图，∵CD=CE﹣DE，
∴BE=AD﹣DE=5﹣3=2（cm），即BE的长度是2cm
【解析】（1）根据全等三角形的判定定理AAS推知：△ADC≌△CEB；（2）利用（1）中的全等三角形的对应边相等得到：AD=CE=5cm，CD=BE．则根据图中相关线段的和差关系得到BE=AD﹣DE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知a，b，c，d都不等于0，并且
， 根据分式的基本性质、等式的基本性质及运算法则，探究下面各组中的两个分式之间有什么关系？然后选择其中一组进行具体说明．
（1）
和
； （2）
和
； （3）
和
（a≠b，c≠d）． -
科目： 来源： 题型：
查看答案和解析>>【题目】求﹣（5a+b﹣ab）﹣（2ab﹣2a﹣4b）+（2b﹣2a﹣3ab） 的值．（其中a﹣b=5，ab=﹣3．）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形网格中，△ABC各顶点都在格点上，点A，C的坐标分别为（﹣5，1）、（﹣1，4），结合所给的平面直角坐标系解答下列问题：
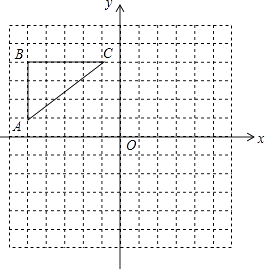
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）画出△ABC关于原点O对称的△A2B2C2；
（3）点C1的坐标是；点C2的坐标是；△ABC的面积是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ＋PQ的最小值是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．
（1）求证：AD=AG；
（2）AD与AG的位置关系如何，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知y=
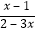， x取哪些值时：（1）y的值是正数；（2）y的值是负数；（3）y的值是零；（4）分式无意义．
相关试题
